DEANN: Speeding up Kernel-Density Estimation using Approximate Nearest Neighbor Search

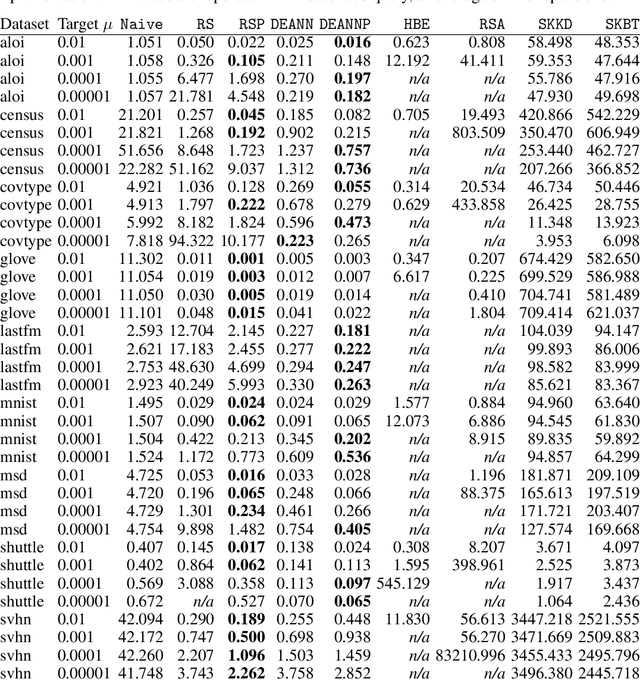
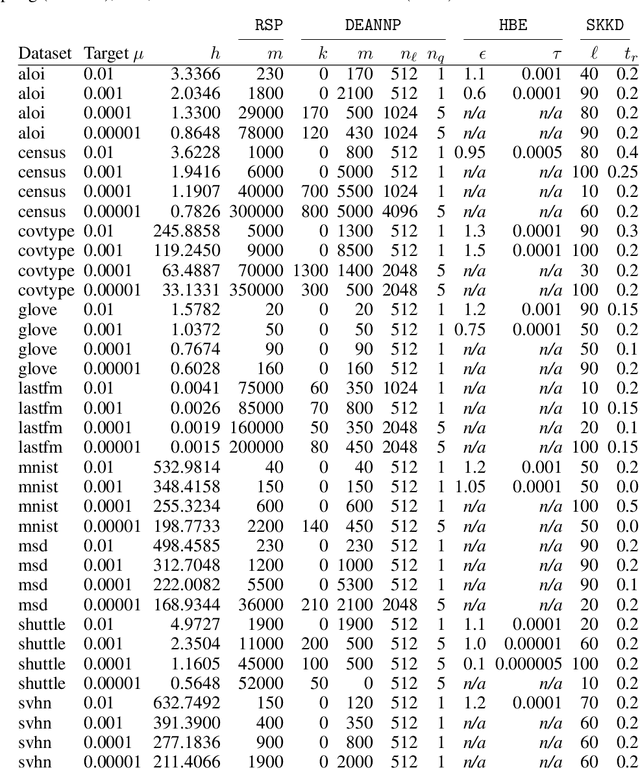
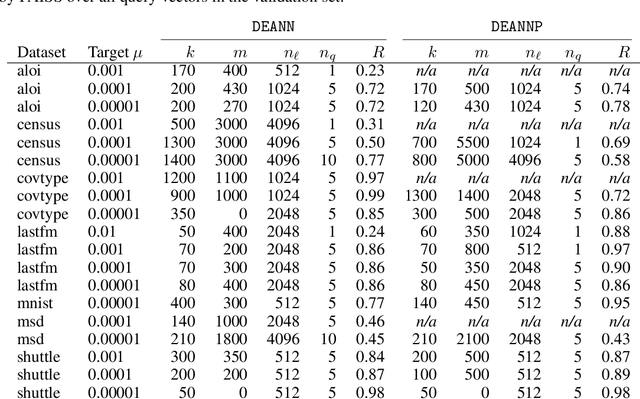
Kernel Density Estimation (KDE) is a nonparametric method for estimating the shape of a density function, given a set of samples from the distribution. Recently, locality-sensitive hashing, originally proposed as a tool for nearest neighbor search, has been shown to enable fast KDE data structures. However, these approaches do not take advantage of the many other advances that have been made in algorithms for nearest neighbor algorithms. We present an algorithm called Density Estimation from Approximate Nearest Neighbors (DEANN) where we apply Approximate Nearest Neighbor (ANN) algorithms as a black box subroutine to compute an unbiased KDE. The idea is to find points that have a large contribution to the KDE using ANN, compute their contribution exactly, and approximate the remainder with Random Sampling (RS). We present a theoretical argument that supports the idea that an ANN subroutine can speed up the evaluation. Furthermore, we provide a C++ implementation with a Python interface that can make use of an arbitrary ANN implementation as a subroutine for KDE evaluation. We show empirically that our implementation outperforms state of the art implementations in all high dimensional datasets we considered, and matches the performance of RS in cases where the ANN yield no gains in performance.

An adaptive prefix-assignment technique for symmetry reduction

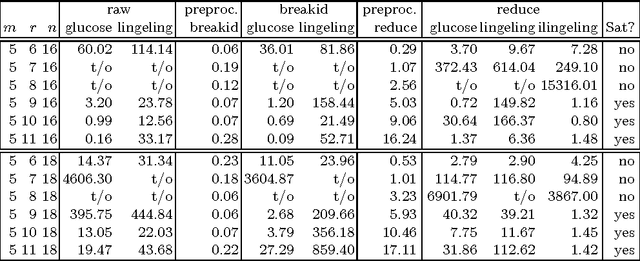
This paper presents a technique for symmetry reduction that adaptively assigns a prefix of variables in a system of constraints so that the generated prefix-assignments are pairwise nonisomorphic under the action of the symmetry group of the system. The technique is based on McKay's canonical extension framework [J.~Algorithms 26 (1998), no.~2, 306--324]. Among key features of the technique are (i) adaptability---the prefix sequence can be user-prescribed and truncated for compatibility with the group of symmetries; (ii) parallelizability---prefix-assignments can be processed in parallel independently of each other; (iii) versatility---the method is applicable whenever the group of symmetries can be concisely represented as the automorphism group of a vertex-colored graph; and (iv) implementability---the method can be implemented relying on a canonical labeling map for vertex-colored graphs as the only nontrivial subroutine. To demonstrate the practical applicability of our technique, we have prepared an experimental open-source implementation of the technique and carry out a set of experiments that demonstrate ability to reduce symmetry on hard instances. Furthermore, we demonstrate that the implementation effectively parallelizes to compute clusters with multiple nodes via a message-passing interface.