An adaptive prefix-assignment technique for symmetry reduction

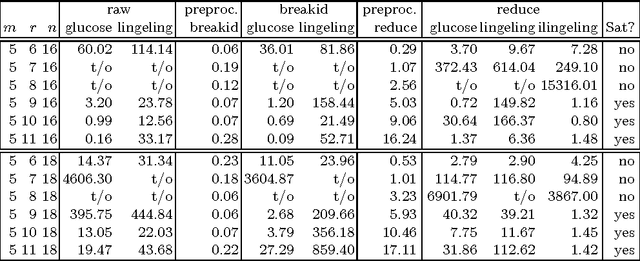
This paper presents a technique for symmetry reduction that adaptively assigns a prefix of variables in a system of constraints so that the generated prefix-assignments are pairwise nonisomorphic under the action of the symmetry group of the system. The technique is based on McKay's canonical extension framework [J.~Algorithms 26 (1998), no.~2, 306--324]. Among key features of the technique are (i) adaptability---the prefix sequence can be user-prescribed and truncated for compatibility with the group of symmetries; (ii) parallelizability---prefix-assignments can be processed in parallel independently of each other; (iii) versatility---the method is applicable whenever the group of symmetries can be concisely represented as the automorphism group of a vertex-colored graph; and (iv) implementability---the method can be implemented relying on a canonical labeling map for vertex-colored graphs as the only nontrivial subroutine. To demonstrate the practical applicability of our technique, we have prepared an experimental open-source implementation of the technique and carry out a set of experiments that demonstrate ability to reduce symmetry on hard instances. Furthermore, we demonstrate that the implementation effectively parallelizes to compute clusters with multiple nodes via a message-passing interface.

Circumspect descent prevails in solving random constraint satisfaction problems

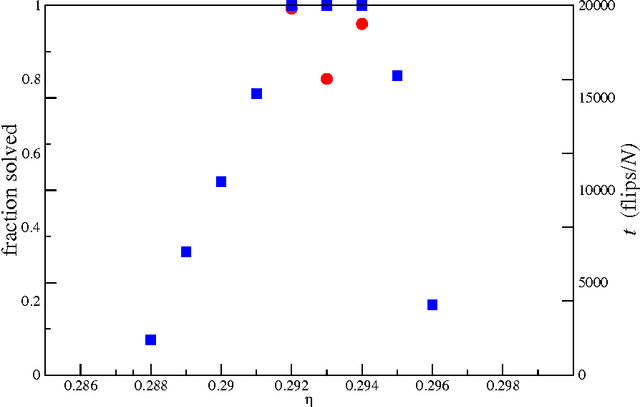
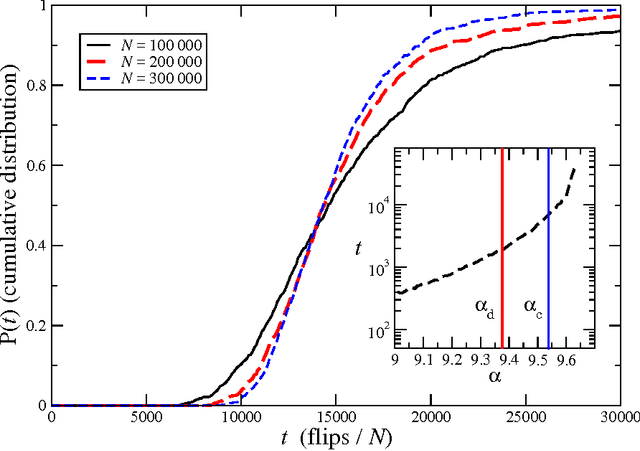
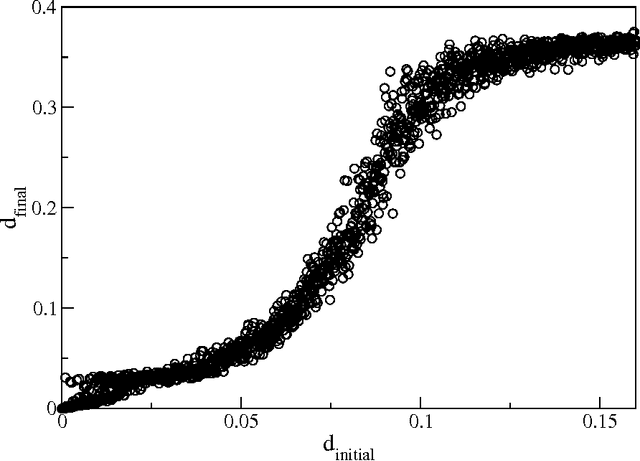
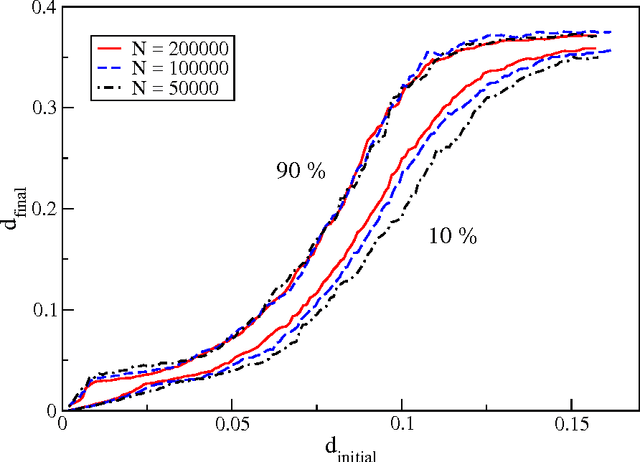
We study the performance of stochastic local search algorithms for random instances of the $K$-satisfiability ($K$-SAT) problem. We introduce a new stochastic local search algorithm, ChainSAT, which moves in the energy landscape of a problem instance by {\em never going upwards} in energy. ChainSAT is a \emph{focused} algorithm in the sense that it considers only variables occurring in unsatisfied clauses. We show by extensive numerical investigations that ChainSAT and other focused algorithms solve large $K$-SAT instances almost surely in linear time, up to high clause-to-variable ratios $\alpha$; for example, for K=4 we observe linear-time performance well beyond the recently postulated clustering and condensation transitions in the solution space. The performance of ChainSAT is a surprise given that by design the algorithm gets trapped into the first local energy minimum it encounters, yet no such minima are encountered. We also study the geometry of the solution space as accessed by stochastic local search algorithms.