Balanced K-SAT and Biased random K-SAT on trees

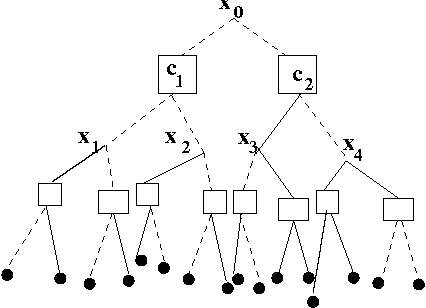
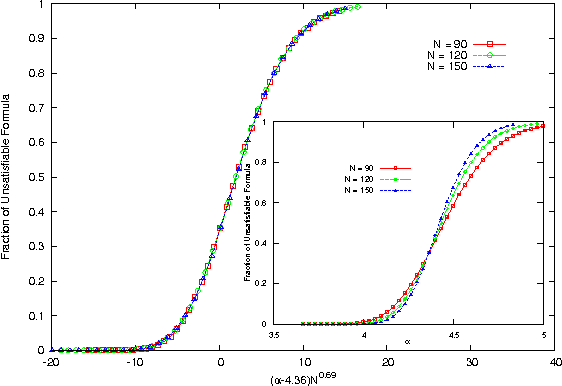
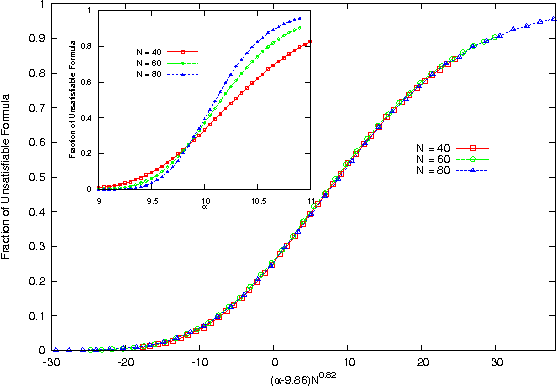
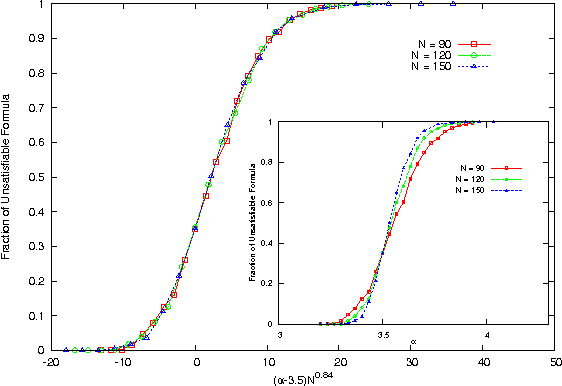
We study and solve some variations of the random K-satisfiability problem - balanced K-SAT and biased random K-SAT - on a regular tree, using techniques we have developed earlier(arXiv:1110.2065). In both these problems, as well as variations of these that we have looked at, we find that the SAT-UNSAT transition obtained on the Bethe lattice matches the exact threshold for the same model on a random graph for K=2 and is very close to the numerical value obtained for K=3. For higher K it deviates from the numerical estimates of the solvability threshold on random graphs, but is very close to the dynamical 1-RSB threshold as obtained from the first non-trivial fixed point of the survey propagation algorithm.

Circumspect descent prevails in solving random constraint satisfaction problems

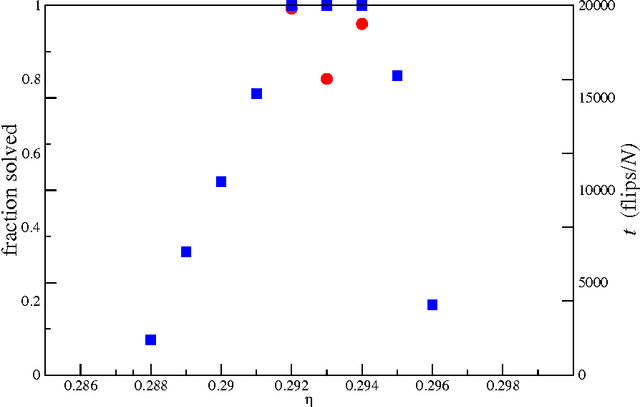
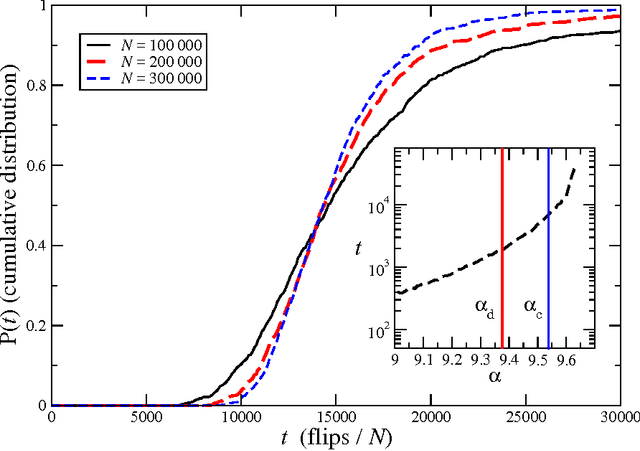
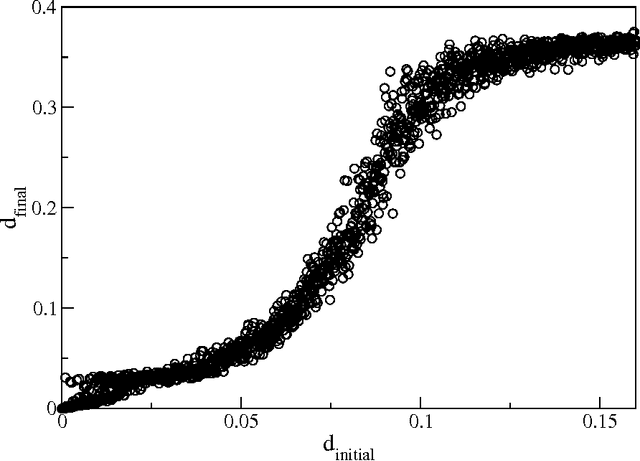
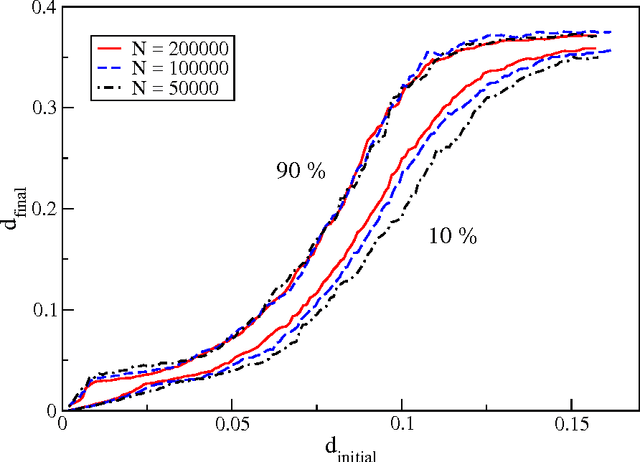
We study the performance of stochastic local search algorithms for random instances of the $K$-satisfiability ($K$-SAT) problem. We introduce a new stochastic local search algorithm, ChainSAT, which moves in the energy landscape of a problem instance by {\em never going upwards} in energy. ChainSAT is a \emph{focused} algorithm in the sense that it considers only variables occurring in unsatisfied clauses. We show by extensive numerical investigations that ChainSAT and other focused algorithms solve large $K$-SAT instances almost surely in linear time, up to high clause-to-variable ratios $\alpha$; for example, for K=4 we observe linear-time performance well beyond the recently postulated clustering and condensation transitions in the solution space. The performance of ChainSAT is a surprise given that by design the algorithm gets trapped into the first local energy minimum it encounters, yet no such minima are encountered. We also study the geometry of the solution space as accessed by stochastic local search algorithms.