Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Sharmistha Sahoo
Balanced K-SAT and Biased random K-SAT on trees
Dec 10, 2012Figures and Tables: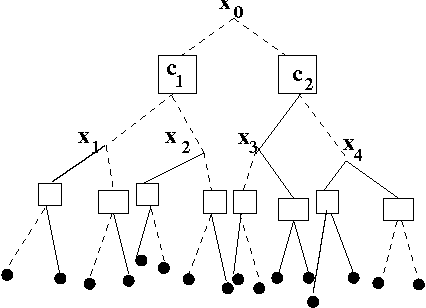
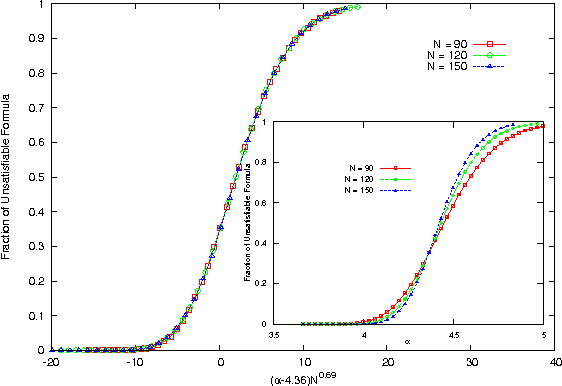
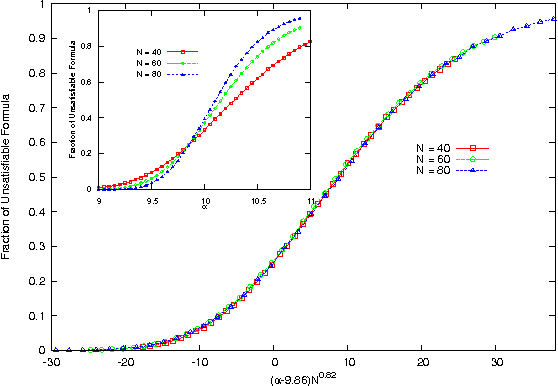
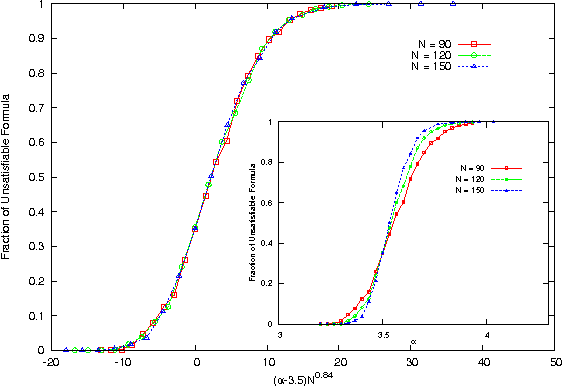




Abstract:We study and solve some variations of the random K-satisfiability problem - balanced K-SAT and biased random K-SAT - on a regular tree, using techniques we have developed earlier(arXiv:1110.2065). In both these problems, as well as variations of these that we have looked at, we find that the SAT-UNSAT transition obtained on the Bethe lattice matches the exact threshold for the same model on a random graph for K=2 and is very close to the numerical value obtained for K=3. For higher K it deviates from the numerical estimates of the solvability threshold on random graphs, but is very close to the dynamical 1-RSB threshold as obtained from the first non-trivial fixed point of the survey propagation algorithm.
* Phys. Rev. E 87, 042130 (2013)
* 22 pages, 7 figures
* 22 pages, 7 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge