A novel local search based on variable-focusing for random K-SAT

We introduce a new local search algorithm for satisfiability problems. Usual approaches focus uniformly on unsatisfied clauses. The new method works by picking uniformly random variables in unsatisfied clauses. A Variable-based Focused Metropolis Search (V-FMS) is then applied to random 3-SAT. We show that it is quite comparable in performance to the clause-based FMS. Consequences for algorithmic design are discussed.

Circumspect descent prevails in solving random constraint satisfaction problems

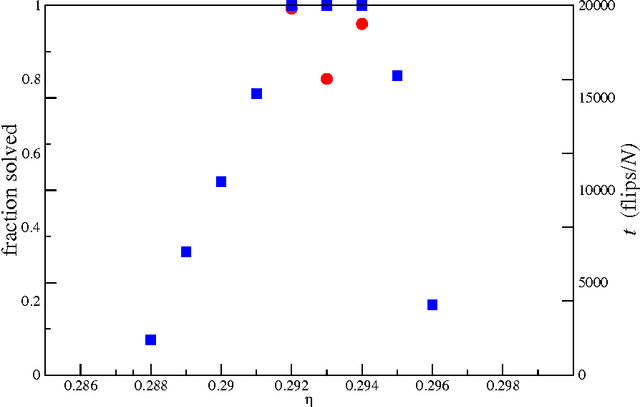
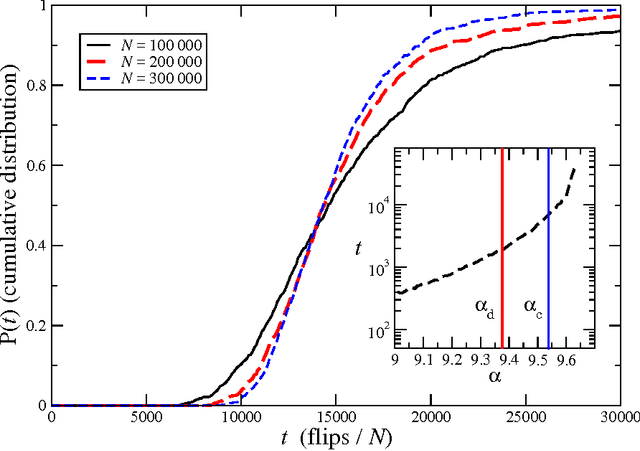
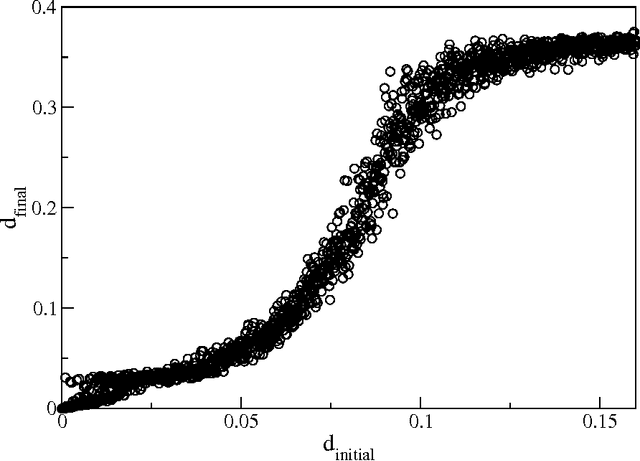
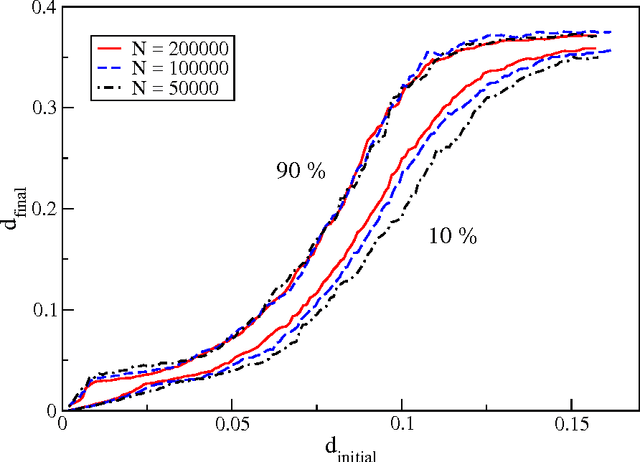
We study the performance of stochastic local search algorithms for random instances of the $K$-satisfiability ($K$-SAT) problem. We introduce a new stochastic local search algorithm, ChainSAT, which moves in the energy landscape of a problem instance by {\em never going upwards} in energy. ChainSAT is a \emph{focused} algorithm in the sense that it considers only variables occurring in unsatisfied clauses. We show by extensive numerical investigations that ChainSAT and other focused algorithms solve large $K$-SAT instances almost surely in linear time, up to high clause-to-variable ratios $\alpha$; for example, for K=4 we observe linear-time performance well beyond the recently postulated clustering and condensation transitions in the solution space. The performance of ChainSAT is a surprise given that by design the algorithm gets trapped into the first local energy minimum it encounters, yet no such minima are encountered. We also study the geometry of the solution space as accessed by stochastic local search algorithms.