Fast $(1+\varepsilon)$-Approximation Algorithms for Binary Matrix Factorization
Paper and Code
Jun 02, 2023
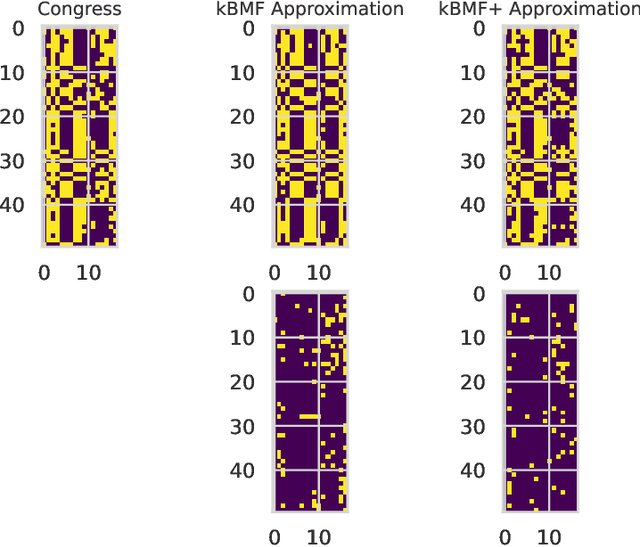

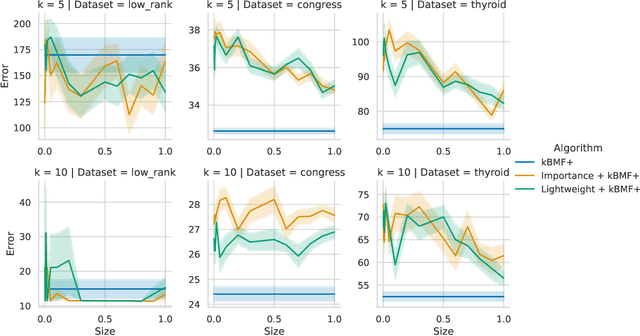
We introduce efficient $(1+\varepsilon)$-approximation algorithms for the binary matrix factorization (BMF) problem, where the inputs are a matrix $\mathbf{A}\in\{0,1\}^{n\times d}$, a rank parameter $k>0$, as well as an accuracy parameter $\varepsilon>0$, and the goal is to approximate $\mathbf{A}$ as a product of low-rank factors $\mathbf{U}\in\{0,1\}^{n\times k}$ and $\mathbf{V}\in\{0,1\}^{k\times d}$. Equivalently, we want to find $\mathbf{U}$ and $\mathbf{V}$ that minimize the Frobenius loss $\|\mathbf{U}\mathbf{V} - \mathbf{A}\|_F^2$. Before this work, the state-of-the-art for this problem was the approximation algorithm of Kumar et. al. [ICML 2019], which achieves a $C$-approximation for some constant $C\ge 576$. We give the first $(1+\varepsilon)$-approximation algorithm using running time singly exponential in $k$, where $k$ is typically a small integer. Our techniques generalize to other common variants of the BMF problem, admitting bicriteria $(1+\varepsilon)$-approximation algorithms for $L_p$ loss functions and the setting where matrix operations are performed in $\mathbb{F}_2$. Our approach can be implemented in standard big data models, such as the streaming or distributed models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge