Relaxed Equivariance via Multitask Learning

Incorporating equivariance as an inductive bias into deep learning architectures to take advantage of the data symmetry has been successful in multiple applications, such as chemistry and dynamical systems. In particular, roto-translations are crucial for effectively modeling geometric graphs and molecules, where understanding the 3D structures enhances generalization. However, equivariant models often pose challenges due to their high computational complexity. In this paper, we introduce REMUL, a training procedure for approximating equivariance with multitask learning. We show that unconstrained models (which do not build equivariance into the architecture) can learn approximate symmetries by minimizing an additional simple equivariance loss. By formulating equivariance as a new learning objective, we can control the level of approximate equivariance in the model. Our method achieves competitive performance compared to equivariant baselines while being $10 \times$ faster at inference and $2.5 \times$ at training.

Metric Flow Matching for Smooth Interpolations on the Data Manifold

Matching objectives underpin the success of modern generative models and rely on constructing conditional paths that transform a source distribution into a target distribution. Despite being a fundamental building block, conditional paths have been designed principally under the assumption of Euclidean geometry, resulting in straight interpolations. However, this can be particularly restrictive for tasks such as trajectory inference, where straight paths might lie outside the data manifold, thus failing to capture the underlying dynamics giving rise to the observed marginals. In this paper, we propose Metric Flow Matching (MFM), a novel simulation-free framework for conditional flow matching where interpolants are approximate geodesics learned by minimizing the kinetic energy of a data-induced Riemannian metric. This way, the generative model matches vector fields on the data manifold, which corresponds to lower uncertainty and more meaningful interpolations. We prescribe general metrics to instantiate MFM, independent of the task, and test it on a suite of challenging problems including LiDAR navigation, unpaired image translation, and modeling cellular dynamics. We observe that MFM outperforms the Euclidean baselines, particularly achieving SOTA on single-cell trajectory prediction.

Understanding Virtual Nodes: Oversmoothing, Oversquashing, and Node Heterogeneity

Message passing neural networks (MPNNs) have been shown to have limitations in terms of expressivity and modeling long-range interactions. Augmenting MPNNs with a virtual node (VN) removes the locality constraint of the layer aggregation and has been found to improve performance on a range of benchmarks. We provide a comprehensive theoretical analysis of the role of VNs and benefits thereof, through the lenses of oversmoothing, oversquashing, and sensitivity analysis. First, in contrast to prior belief, we find that VNs typically avoid replicating anti-smoothing approaches to maintain expressive power. Second, we characterize, precisely, how the improvement afforded by VNs on the mixing abilities of the network and hence in mitigating oversquashing, depends on the underlying topology. Finally, we highlight that, unlike Graph-Transformers (GT), classical instantiations of the VN are often constrained to assign uniform importance to different nodes. Consequently, we propose a variant of VN with the same computational complexity, which can have different sensitivity to nodes based on the graph structure. We show that this is an extremely effective and computationally efficient baseline on graph-level tasks.

Advancing Graph Convolutional Networks via General Spectral Wavelets

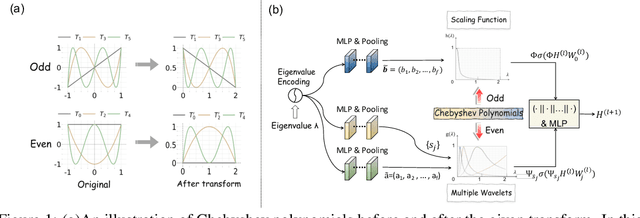
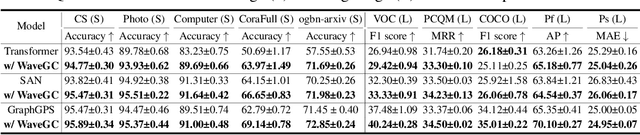
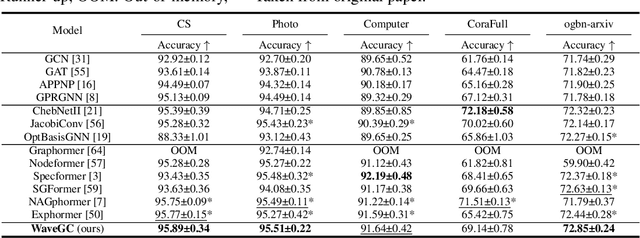
Spectral graph convolution, an important tool of data filtering on graphs, relies on two essential decisions; selecting spectral bases for signal transformation and parameterizing the kernel for frequency analysis. While recent techniques mainly focus on standard Fourier transform and vector-valued spectral functions, they fall short in flexibility to describe specific signal distribution for each node, and expressivity of spectral function. In this paper, we present a novel wavelet-based graph convolution network, namely WaveGC, which integrates multi-resolution spectral bases and a matrix-valued filter kernel. Theoretically, we establish that WaveGC can effectively capture and decouple short-range and long-range information, providing superior filtering flexibility, surpassing existing graph convolutional networks and graph Transformers (GTs). To instantiate WaveGC, we introduce a novel technique for learning general graph wavelets by separately combining odd and even terms of Chebyshev polynomials. This approach strictly satisfies wavelet admissibility criteria. Our numerical experiments showcase the capabilities of the new network. By replacing the Transformer part in existing architectures with WaveGC, we consistently observe improvements in both short-range and long-range tasks. This underscores the effectiveness of the proposed model in handling different scenarios. Our code is available at https://github.com/liun-online/WaveGC.

Can strong structural encoding reduce the importance of Message Passing?

The most prevalent class of neural networks operating on graphs are message passing neural networks (MPNNs), in which the representation of a node is updated iteratively by aggregating information in the 1-hop neighborhood. Since this paradigm for computing node embeddings may prevent the model from learning coarse topological structures, the initial features are often augmented with structural information of the graph, typically in the form of Laplacian eigenvectors or Random Walk transition probabilities. In this work, we explore the contribution of message passing when strong structural encodings are provided. We introduce a novel way of modeling the interaction between feature and structural information based on their tensor product rather than the standard concatenation. The choice of interaction is compared in common scenarios and in settings where the capacity of the message-passing layer is severely reduced and ultimately the message-passing phase is removed altogether. Our results indicate that using tensor-based encodings is always at least on par with the concatenation-based encoding and that it makes the model much more robust when the message passing layers are removed, on some tasks incurring almost no drop in performance. This suggests that the importance of message passing is limited when the model can construct strong structural encodings.

Locality-Aware Graph-Rewiring in GNNs

Graph Neural Networks (GNNs) are popular models for machine learning on graphs that typically follow the message-passing paradigm, whereby the feature of a node is updated recursively upon aggregating information over its neighbors. While exchanging messages over the input graph endows GNNs with a strong inductive bias, it can also make GNNs susceptible to over-squashing, thereby preventing them from capturing long-range interactions in the given graph. To rectify this issue, graph rewiring techniques have been proposed as a means of improving information flow by altering the graph connectivity. In this work, we identify three desiderata for graph-rewiring: (i) reduce over-squashing, (ii) respect the locality of the graph, and (iii) preserve the sparsity of the graph. We highlight fundamental trade-offs that occur between spatial and spectral rewiring techniques; while the former often satisfy (i) and (ii) but not (iii), the latter generally satisfy (i) and (iii) at the expense of (ii). We propose a novel rewiring framework that satisfies all of (i)--(iii) through a locality-aware sequence of rewiring operations. We then discuss a specific instance of such rewiring framework and validate its effectiveness on several real-world benchmarks, showing that it either matches or significantly outperforms existing rewiring approaches.

How does over-squashing affect the power of GNNs?

Graph Neural Networks (GNNs) are the state-of-the-art model for machine learning on graph-structured data. The most popular class of GNNs operate by exchanging information between adjacent nodes, and are known as Message Passing Neural Networks (MPNNs). Given their widespread use, understanding the expressive power of MPNNs is a key question. However, existing results typically consider settings with uninformative node features. In this paper, we provide a rigorous analysis to determine which function classes of node features can be learned by an MPNN of a given capacity. We do so by measuring the level of pairwise interactions between nodes that MPNNs allow for. This measure provides a novel quantitative characterization of the so-called over-squashing effect, which is observed to occur when a large volume of messages is aggregated into fixed-size vectors. Using our measure, we prove that, to guarantee sufficient communication between pairs of nodes, the capacity of the MPNN must be large enough, depending on properties of the input graph structure, such as commute times. For many relevant scenarios, our analysis results in impossibility statements in practice, showing that over-squashing hinders the expressive power of MPNNs. We validate our theoretical findings through extensive controlled experiments and ablation studies.

DRew: Dynamically Rewired Message Passing with Delay

Message passing neural networks (MPNNs) have been shown to suffer from the phenomenon of over-squashing that causes poor performance for tasks relying on long-range interactions. This can be largely attributed to message passing only occurring locally, over a node's immediate neighbours. Rewiring approaches attempting to make graphs 'more connected', and supposedly better suited to long-range tasks, often lose the inductive bias provided by distance on the graph since they make distant nodes communicate instantly at every layer. In this paper we propose a framework, applicable to any MPNN architecture, that performs a layer-dependent rewiring to ensure gradual densification of the graph. We also propose a delay mechanism that permits skip connections between nodes depending on the layer and their mutual distance. We validate our approach on several long-range tasks and show that it outperforms graph Transformers and multi-hop MPNNs.

Edge Directionality Improves Learning on Heterophilic Graphs

Graph Neural Networks (GNNs) have become the de-facto standard tool for modeling relational data. However, while many real-world graphs are directed, the majority of today's GNN models discard this information altogether by simply making the graph undirected. The reasons for this are historical: 1) many early variants of spectral GNNs explicitly required undirected graphs, and 2) the first benchmarks on homophilic graphs did not find significant gain from using direction. In this paper, we show that in heterophilic settings, treating the graph as directed increases the effective homophily of the graph, suggesting a potential gain from the correct use of directionality information. To this end, we introduce Directed Graph Neural Network (Dir-GNN), a novel general framework for deep learning on directed graphs. Dir-GNN can be used to extend any Message Passing Neural Network (MPNN) to account for edge directionality information by performing separate aggregations of the incoming and outgoing edges. We prove that Dir-GNN matches the expressivity of the Directed Weisfeiler-Lehman test, exceeding that of conventional MPNNs. In extensive experiments, we validate that while our framework leaves performance unchanged on homophilic datasets, it leads to large gains over base models such as GCN, GAT and GraphSage on heterophilic benchmarks, outperforming much more complex methods and achieving new state-of-the-art results.

On Over-Squashing in Message Passing Neural Networks: The Impact of Width, Depth, and Topology

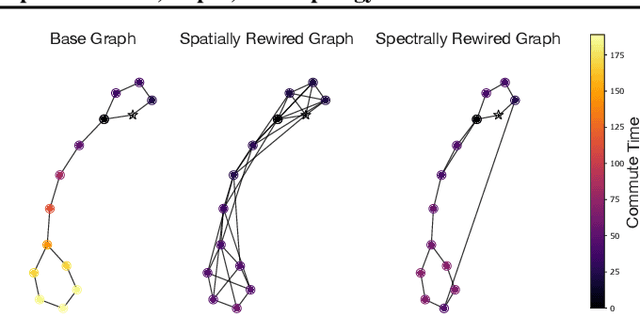
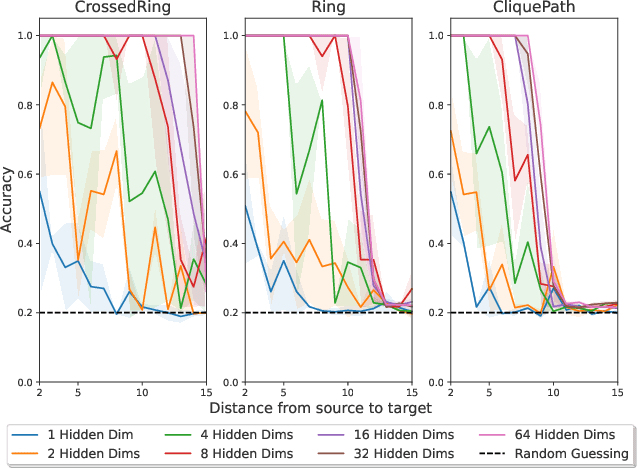
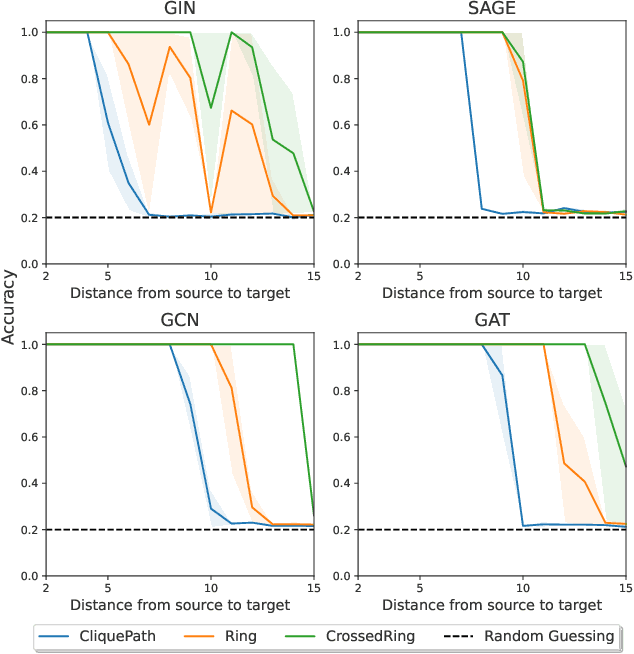
Message Passing Neural Networks (MPNNs) are instances of Graph Neural Networks that leverage the graph to send messages over the edges. This inductive bias leads to a phenomenon known as over-squashing, where a node feature is insensitive to information contained at distant nodes. Despite recent methods introduced to mitigate this issue, an understanding of the causes for over-squashing and of possible solutions are lacking. In this theoretical work, we prove that: (i) Neural network width can mitigate over-squashing, but at the cost of making the whole network more sensitive; (ii) Conversely, depth cannot help mitigate over-squashing: increasing the number of layers leads to over-squashing being dominated by vanishing gradients; (iii) The graph topology plays the greatest role, since over-squashing occurs between nodes at high commute (access) time. Our analysis provides a unified framework to study different recent methods introduced to cope with over-squashing and serves as a justification for a class of methods that fall under `graph rewiring'.