Advancing Graph Convolutional Networks via General Spectral Wavelets
Paper and Code
May 22, 2024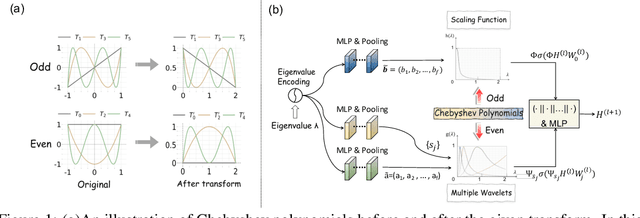

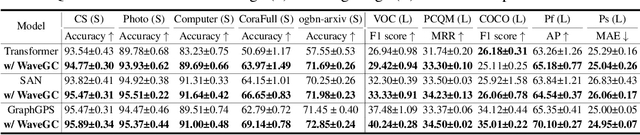
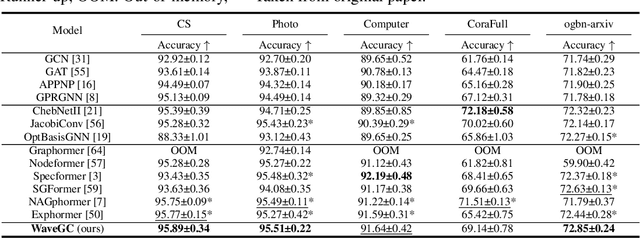
Spectral graph convolution, an important tool of data filtering on graphs, relies on two essential decisions; selecting spectral bases for signal transformation and parameterizing the kernel for frequency analysis. While recent techniques mainly focus on standard Fourier transform and vector-valued spectral functions, they fall short in flexibility to describe specific signal distribution for each node, and expressivity of spectral function. In this paper, we present a novel wavelet-based graph convolution network, namely WaveGC, which integrates multi-resolution spectral bases and a matrix-valued filter kernel. Theoretically, we establish that WaveGC can effectively capture and decouple short-range and long-range information, providing superior filtering flexibility, surpassing existing graph convolutional networks and graph Transformers (GTs). To instantiate WaveGC, we introduce a novel technique for learning general graph wavelets by separately combining odd and even terms of Chebyshev polynomials. This approach strictly satisfies wavelet admissibility criteria. Our numerical experiments showcase the capabilities of the new network. By replacing the Transformer part in existing architectures with WaveGC, we consistently observe improvements in both short-range and long-range tasks. This underscores the effectiveness of the proposed model in handling different scenarios. Our code is available at https://github.com/liun-online/WaveGC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge