Federated GNNs for EEG-Based Stroke Assessment

Machine learning (ML) has the potential to become an essential tool in supporting clinical decision-making processes, offering enhanced diagnostic capabilities and personalized treatment plans. However, outsourcing medical records to train ML models using patient data raises legal, privacy, and security concerns. Federated learning has emerged as a promising paradigm for collaborative ML, meeting healthcare institutions' requirements for robust models without sharing sensitive data and compromising patient privacy. This study proposes a novel method that combines federated learning (FL) and Graph Neural Networks (GNNs) to predict stroke severity using electroencephalography (EEG) signals across multiple medical institutions. Our approach enables multiple hospitals to jointly train a shared GNN model on their local EEG data without exchanging patient information. Specifically, we address a regression problem by predicting the National Institutes of Health Stroke Scale (NIHSS), a key indicator of stroke severity. The proposed model leverages a masked self-attention mechanism to capture salient brain connectivity patterns and employs EdgeSHAP to provide post-hoc explanations of the neurological states after a stroke. We evaluated our method on EEG recordings from four institutions, achieving a mean absolute error (MAE) of 3.23 in predicting NIHSS, close to the average error made by human experts (MAE $\approx$ 3.0). This demonstrates the method's effectiveness in providing accurate and explainable predictions while maintaining data privacy.

Topological Neural Networks: Mitigating the Bottlenecks of Graph Neural Networks via Higher-Order Interactions

The irreducible complexity of natural phenomena has led Graph Neural Networks to be employed as a standard model to perform representation learning tasks on graph-structured data. While their capacity to capture local and global patterns is remarkable, the implications associated with long-range and higher-order dependencies pose considerable challenges to such models. This work starts with a theoretical framework to reveal the impact of network's width, depth, and graph topology on the over-squashing phenomena in message-passing neural networks. Then, the work drifts towards, higher-order interactions and multi-relational inductive biases via Topological Neural Networks. Such models propagate messages through higher-dimensional structures, providing shortcuts or additional routes for information flow. With this construction, the underlying computational graph is no longer coupled with the input graph structure, thus mitigating the aforementioned bottlenecks while accounting also for higher-order interactions. Inspired by Graph Attention Networks, two topological attention networks are proposed: Simplicial and Cell Attention Networks. The rationale behind these architecture is to leverage the extended notion of neighbourhoods provided by the arrangement of groups of nodes within a simplicial or cell complex to design anisotropic aggregations able to measure the importance of the information coming from different regions of the domain. By doing so, they capture dependencies that conventional Graph Neural Networks might miss. Finally, a multi-way communication scheme is introduced with Enhanced Cellular Isomorphism Networks, which augment topological message passing schemes to enable a direct interactions among groups of nodes arranged in ring-like structures.

Generalized Simplicial Attention Neural Networks

The aim of this work is to introduce Generalized Simplicial Attention Neural Networks (GSANs), i.e., novel neural architectures designed to process data defined on simplicial complexes using masked self-attentional layers. Hinging on topological signal processing principles, we devise a series of self-attention schemes capable of processing data components defined at different simplicial orders, such as nodes, edges, triangles, and beyond. These schemes learn how to weight the neighborhoods of the given topological domain in a task-oriented fashion, leveraging the interplay among simplices of different orders through the Dirac operator and its Dirac decomposition. We also theoretically establish that GSANs are permutation equivariant and simplicial-aware. Finally, we illustrate how our approach compares favorably with other methods when applied to several (inductive and transductive) tasks such as trajectory prediction, missing data imputation, graph classification, and simplex prediction.

Neural Embeddings for Protein Graphs

Proteins perform much of the work in living organisms, and consequently the development of efficient computational methods for protein representation is essential for advancing large-scale biological research. Most current approaches struggle to efficiently integrate the wealth of information contained in the protein sequence and structure. In this paper, we propose a novel framework for embedding protein graphs in geometric vector spaces, by learning an encoder function that preserves the structural distance between protein graphs. Utilizing Graph Neural Networks (GNNs) and Large Language Models (LLMs), the proposed framework generates structure- and sequence-aware protein representations. We demonstrate that our embeddings are successful in the task of comparing protein structures, while providing a significant speed-up compared to traditional approaches based on structural alignment. Our framework achieves remarkable results in the task of protein structure classification; in particular, when compared to other work, the proposed method shows an average F1-Score improvement of 26% on out-of-distribution (OOD) samples and of 32% when tested on samples coming from the same distribution as the training data. Our approach finds applications in areas such as drug prioritization, drug re-purposing, disease sub-type analysis and elsewhere.

CIN++: Enhancing Topological Message Passing

Graph Neural Networks (GNNs) have demonstrated remarkable success in learning from graph-structured data. However, they face significant limitations in expressive power, struggling with long-range interactions and lacking a principled approach to modeling higher-order structures and group interactions. Cellular Isomorphism Networks (CINs) recently addressed most of these challenges with a message passing scheme based on cell complexes. Despite their advantages, CINs make use only of boundary and upper messages which do not consider a direct interaction between the rings present in the underlying complex. Accounting for these interactions might be crucial for learning representations of many real-world complex phenomena such as the dynamics of supramolecular assemblies, neural activity within the brain, and gene regulation processes. In this work, we propose CIN++, an enhancement of the topological message passing scheme introduced in CINs. Our message passing scheme accounts for the aforementioned limitations by letting the cells to receive also lower messages within each layer. By providing a more comprehensive representation of higher-order and long-range interactions, our enhanced topological message passing scheme achieves state-of-the-art results on large-scale and long-range chemistry benchmarks.

On Over-Squashing in Message Passing Neural Networks: The Impact of Width, Depth, and Topology

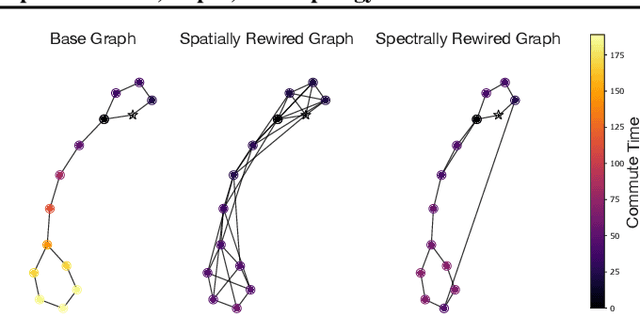
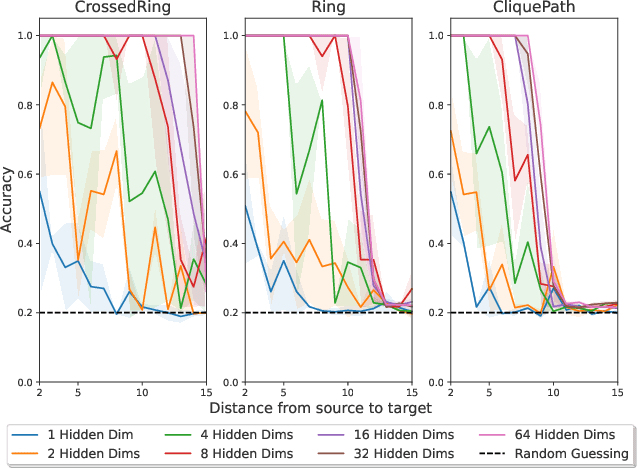
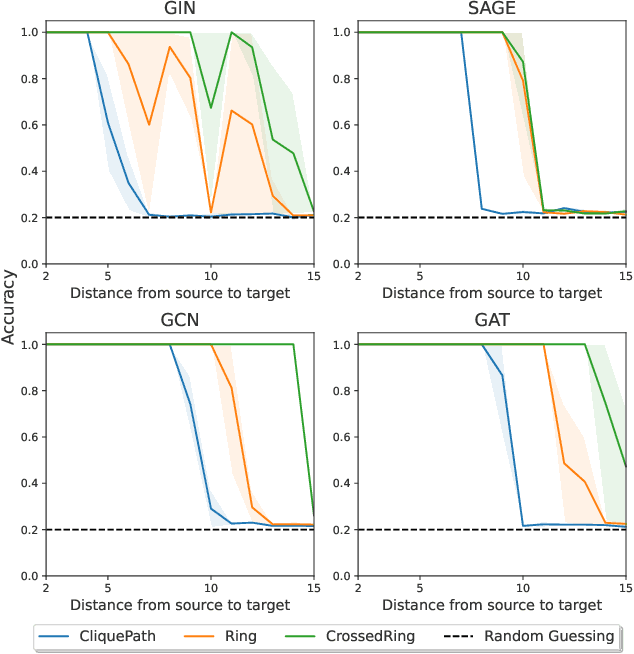
Message Passing Neural Networks (MPNNs) are instances of Graph Neural Networks that leverage the graph to send messages over the edges. This inductive bias leads to a phenomenon known as over-squashing, where a node feature is insensitive to information contained at distant nodes. Despite recent methods introduced to mitigate this issue, an understanding of the causes for over-squashing and of possible solutions are lacking. In this theoretical work, we prove that: (i) Neural network width can mitigate over-squashing, but at the cost of making the whole network more sensitive; (ii) Conversely, depth cannot help mitigate over-squashing: increasing the number of layers leads to over-squashing being dominated by vanishing gradients; (iii) The graph topology plays the greatest role, since over-squashing occurs between nodes at high commute (access) time. Our analysis provides a unified framework to study different recent methods introduced to cope with over-squashing and serves as a justification for a class of methods that fall under `graph rewiring'.

MaRF: Representing Mars as Neural Radiance Fields

The aim of this work is to introduce MaRF, a novel framework able to synthesize the Martian environment using several collections of images from rover cameras. The idea is to generate a 3D scene of Mars' surface to address key challenges in planetary surface exploration such as: planetary geology, simulated navigation and shape analysis. Although there exist different methods to enable a 3D reconstruction of Mars' surface, they rely on classical computer graphics techniques that incur high amounts of computational resources during the reconstruction process, and have limitations with generalizing reconstructions to unseen scenes and adapting to new images coming from rover cameras. The proposed framework solves the aforementioned limitations by exploiting Neural Radiance Fields (NeRFs), a method that synthesize complex scenes by optimizing a continuous volumetric scene function using a sparse set of images. To speed up the learning process, we replaced the sparse set of rover images with their neural graphics primitives (NGPs), a set of vectors of fixed length that are learned to preserve the information of the original images in a significantly smaller size. In the experimental section, we demonstrate the environments created from actual Mars datasets captured by Curiosity rover, Perseverance rover and Ingenuity helicopter, all of which are available on the Planetary Data System (PDS).

Cell Attention Networks

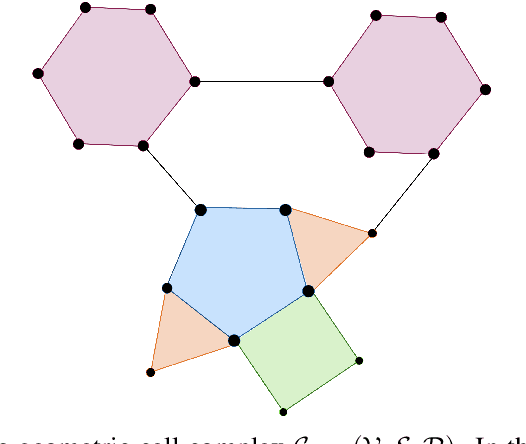
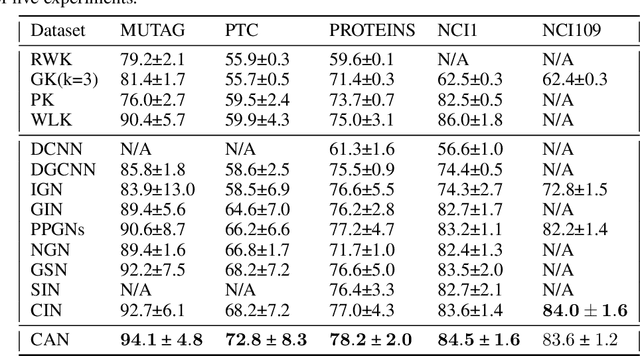
Since their introduction, graph attention networks achieved outstanding results in graph representation learning tasks. However, these networks consider only pairwise relationships among nodes and then they are not able to fully exploit higher-order interactions present in many real world data-sets. In this paper, we introduce Cell Attention Networks (CANs), a neural architecture operating on data defined over the vertices of a graph, representing the graph as the 1-skeleton of a cell complex introduced to capture higher order interactions. In particular, we exploit the lower and upper neighborhoods, as encoded in the cell complex, to design two independent masked self-attention mechanisms, thus generalizing the conventional graph attention strategy. The approach used in CANs is hierarchical and it incorporates the following steps: i) a lifting algorithm that learns {\it edge features} from {\it node features}; ii) a cell attention mechanism to find the optimal combination of edge features over both lower and upper neighbors; iii) a hierarchical {\it edge pooling} mechanism to extract a compact meaningful set of features. The experimental results show that CAN is a low complexity strategy that compares favorably with state of the art results on graph-based learning tasks.