VitaGraph: Building a Knowledge Graph for Biologically Relevant Learning Tasks

The intrinsic complexity of human biology presents ongoing challenges to scientific understanding. Researchers collaborate across disciplines to expand our knowledge of the biological interactions that define human life. AI methodologies have emerged as powerful tools across scientific domains, particularly in computational biology, where graph data structures effectively model biological entities such as protein-protein interaction (PPI) networks and gene functional networks. Those networks are used as datasets for paramount network medicine tasks, such as gene-disease association prediction, drug repurposing, and polypharmacy side effect studies. Reliable predictions from machine learning models require high-quality foundational data. In this work, we present a comprehensive multi-purpose biological knowledge graph constructed by integrating and refining multiple publicly available datasets. Building upon the Drug Repurposing Knowledge Graph (DRKG), we define a pipeline tasked with a) cleaning inconsistencies and redundancies present in DRKG, b) coalescing information from the main available public data sources, and c) enriching the graph nodes with expressive feature vectors such as molecular fingerprints and gene ontologies. Biologically and chemically relevant features improve the capacity of machine learning models to generate accurate and well-structured embedding spaces. The resulting resource represents a coherent and reliable biological knowledge graph that serves as a state-of-the-art platform to advance research in computational biology and precision medicine. Moreover, it offers the opportunity to benchmark graph-based machine learning and network medicine models on relevant tasks. We demonstrate the effectiveness of the proposed dataset by benchmarking it against the task of drug repurposing, PPI prediction, and side-effect prediction, modeled as link prediction problems.

Stability of Graph Convolutional Neural Networks through the lens of small perturbation analysis

In this work, we study the problem of stability of Graph Convolutional Neural Networks (GCNs) under random small perturbations in the underlying graph topology, i.e. under a limited number of insertions or deletions of edges. We derive a novel bound on the expected difference between the outputs of unperturbed and perturbed GCNs. The proposed bound explicitly depends on the magnitude of the perturbation of the eigenpairs of the Laplacian matrix, and the perturbation explicitly depends on which edges are inserted or deleted. Then, we provide a quantitative characterization of the effect of perturbing specific edges on the stability of the network. We leverage tools from small perturbation analysis to express the bounds in closed, albeit approximate, form, in order to enhance interpretability of the results, without the need to compute any perturbed shift operator. Finally, we numerically evaluate the effectiveness of the proposed bound.

ICML 2023 Topological Deep Learning Challenge : Design and Results

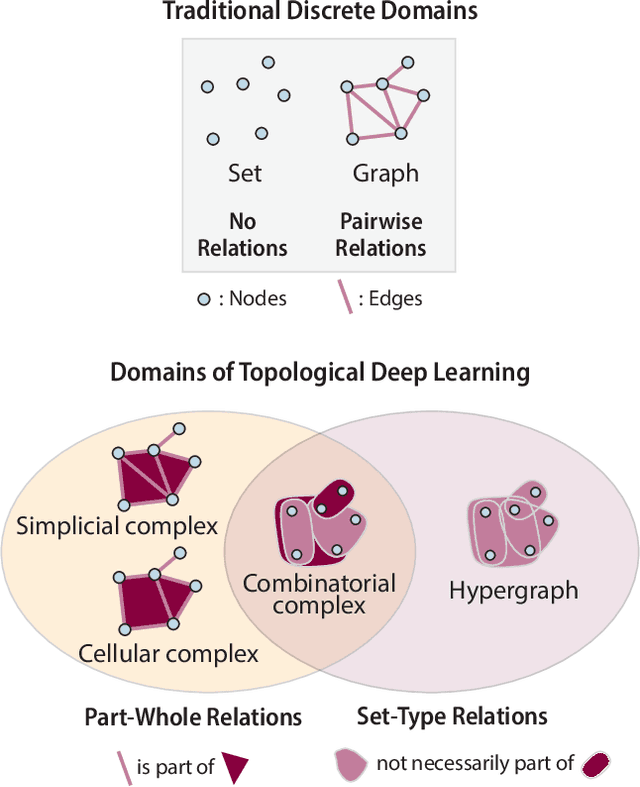
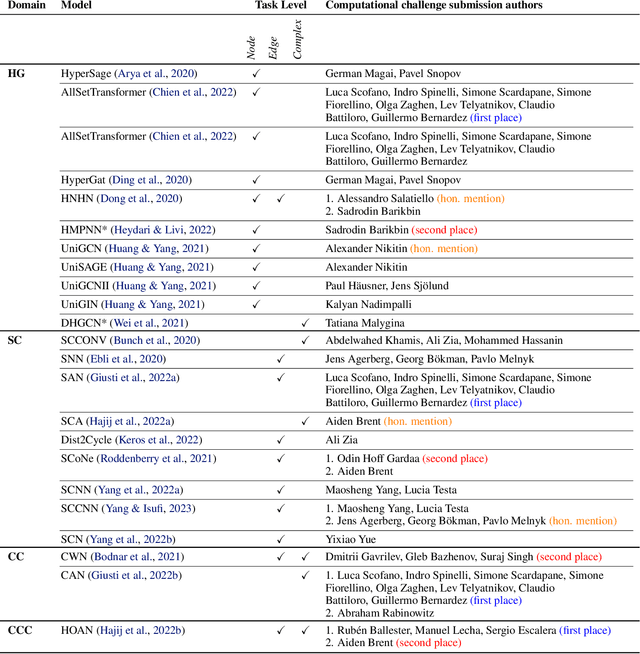
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Generalized Simplicial Attention Neural Networks

The aim of this work is to introduce Generalized Simplicial Attention Neural Networks (GSANs), i.e., novel neural architectures designed to process data defined on simplicial complexes using masked self-attentional layers. Hinging on topological signal processing principles, we devise a series of self-attention schemes capable of processing data components defined at different simplicial orders, such as nodes, edges, triangles, and beyond. These schemes learn how to weight the neighborhoods of the given topological domain in a task-oriented fashion, leveraging the interplay among simplices of different orders through the Dirac operator and its Dirac decomposition. We also theoretically establish that GSANs are permutation equivariant and simplicial-aware. Finally, we illustrate how our approach compares favorably with other methods when applied to several (inductive and transductive) tasks such as trajectory prediction, missing data imputation, graph classification, and simplex prediction.

Cell Attention Networks

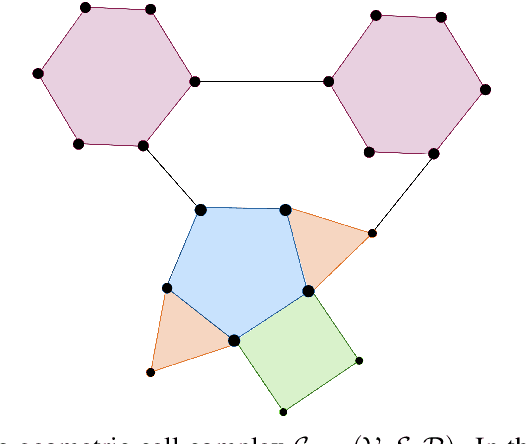
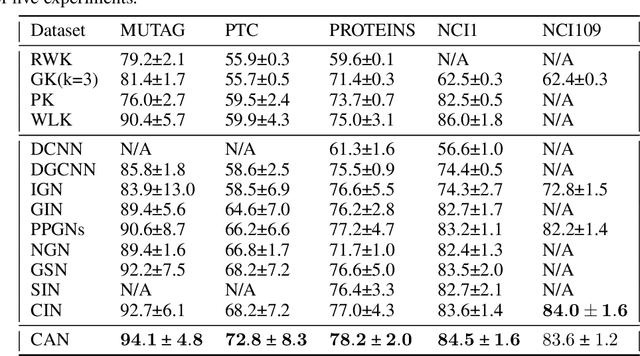
Since their introduction, graph attention networks achieved outstanding results in graph representation learning tasks. However, these networks consider only pairwise relationships among nodes and then they are not able to fully exploit higher-order interactions present in many real world data-sets. In this paper, we introduce Cell Attention Networks (CANs), a neural architecture operating on data defined over the vertices of a graph, representing the graph as the 1-skeleton of a cell complex introduced to capture higher order interactions. In particular, we exploit the lower and upper neighborhoods, as encoded in the cell complex, to design two independent masked self-attention mechanisms, thus generalizing the conventional graph attention strategy. The approach used in CANs is hierarchical and it incorporates the following steps: i) a lifting algorithm that learns {\it edge features} from {\it node features}; ii) a cell attention mechanism to find the optimal combination of edge features over both lower and upper neighbors; iii) a hierarchical {\it edge pooling} mechanism to extract a compact meaningful set of features. The experimental results show that CAN is a low complexity strategy that compares favorably with state of the art results on graph-based learning tasks.

Topological Signal Processing over Cell Complexes

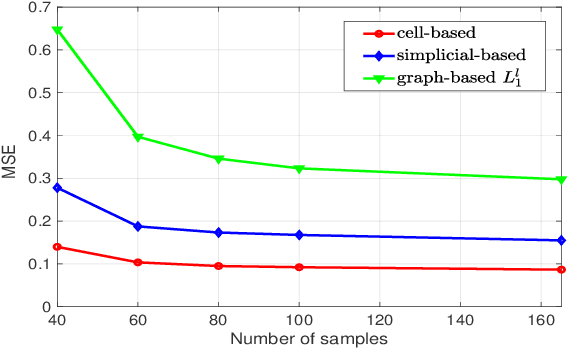
The Topological Signal Processing (TSP) framework has been recently developed to analyze signals defined over simplicial complexes, i.e. topological spaces represented by finite sets of elements that are closed under inclusion of subsets [1]. However, the same inclusion property represents sometimes a too rigid assumption that prevents the application of simplicial complexes to many cases of interest. The goal of this paper is to extend TSP to the analysis of signals defined over cell complexes, which represent a generalization of simplicial complexes, as they are not restricted to satisfy the inclusion property. In particular, the richer topological structure of cell complexes enables them to reveal cycles of any order, as representative of data features. We propose an efficient method to infer the topology of cell complexes from data by showing how their use enables sparser edge signal representations than simplicial-based methods. Furthermore, we show how to design optimal finite impulse response (FIR) filters operating on solenoidal and irrotational signals in order to minimize the approximation error with respect to the desired spectral masks.