Topological Signal Processing over Cell Complexes
Paper and Code
Dec 13, 2021
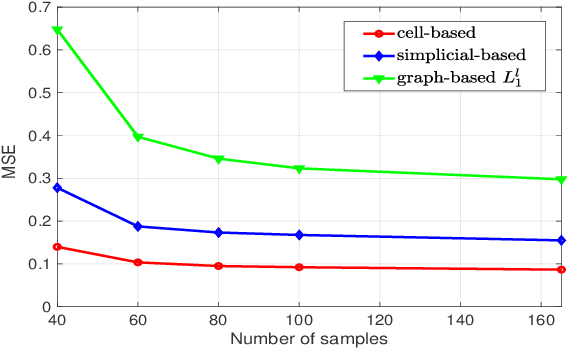

The Topological Signal Processing (TSP) framework has been recently developed to analyze signals defined over simplicial complexes, i.e. topological spaces represented by finite sets of elements that are closed under inclusion of subsets [1]. However, the same inclusion property represents sometimes a too rigid assumption that prevents the application of simplicial complexes to many cases of interest. The goal of this paper is to extend TSP to the analysis of signals defined over cell complexes, which represent a generalization of simplicial complexes, as they are not restricted to satisfy the inclusion property. In particular, the richer topological structure of cell complexes enables them to reveal cycles of any order, as representative of data features. We propose an efficient method to infer the topology of cell complexes from data by showing how their use enables sparser edge signal representations than simplicial-based methods. Furthermore, we show how to design optimal finite impulse response (FIR) filters operating on solenoidal and irrotational signals in order to minimize the approximation error with respect to the desired spectral masks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge