Physics-Informed Topological Signal Processing for Water Distribution Network Monitoring

Water management is one of the most critical aspects of our society, together with population increase and climate change. Water scarcity requires a better characterization and monitoring of Water Distribution Networks (WDNs). This paper presents a novel framework for monitoring Water Distribution Networks (WDNs) by integrating physics-informed modeling of the nonlinear interactions between pressure and flow data with Topological Signal Processing (TSP) techniques. We represent pressure and flow data as signals defined over a second-order cell complex, enabling accurate estimation of water pressures and flows throughout the entire network from sparse sensor measurements. By formalizing hydraulic conservation laws through the TSP framework, we provide a comprehensive representation of nodal pressures and edge flows that incorporate higher-order interactions captured through the formalism of cell complexes. This provides a principled way to decompose the water flows in WDNs in three orthogonal signal components (irrotational, solenoidal and harmonic). The spectral representations of these components inherently reflect the conservation laws governing the water pressures and flows. Sparse representation in the spectral domain enable topology-based sampling and reconstruction of nodal pressures and water flows from sparse measurements. Our results demonstrate that employing cell complex-based signal representations enhances the accuracy of edge signal reconstruction, due to proper modeling of both conservative and non-conservative flows along the polygonal cells.

Cross-Laplacians Based Topological Signal Processing over Cell MultiComplexes

The study of the interactions among different types of interconnected systems in complex networks has attracted significant interest across many research fields. However, effective signal processing over layered networks requires topological descriptors of the intra- and cross-layers relationships that are able to disentangle the homologies of different domains, at different scales, according to the specific learning task. In this paper, we present Cell MultiComplex (CMC) spaces, which are novel topological domains for representing multiple higher-order relationships among interconnected complexes. We introduce cross-Laplacians matrices, which are algebraic descriptors of CMCs enabling the extraction of topological invariants at different scales, whether global or local, inter-layer or intra-layer. Using the eigenvectors of these cross-Laplacians as signal bases, we develop topological signal processing tools for CMC spaces. In this first study, we focus on the representation and filtering of noisy flows observed over cross-edges between different layers of CMCs to identify cross-layer hubs, i.e., key nodes on one layer controlling the others.

Learning Higher-Order Interactions in Brain Networks via Topological Signal Processing

Our goal in this paper is to leverage the potential of the topological signal processing (TSP) framework for analyzing brain networks. Representing brain data as signals over simplicial complexes allows us to capture higher-order relationships within brain regions of interest (ROIs). Here, we focus on learning the underlying brain topology from observed neural signals using two distinct inference strategies. The first method relies on higher-order statistical metrics to infer multiway relationships among ROIs. The second method jointly learns the brain topology and sparse signal representations, of both the solenoidal and harmonic components of the signals, by minimizing the total variation along triangles and the data-fitting errors. Leveraging the properties of solenoidal and irrotational signals, and their physical interpretations, we extract functional connectivity features from brain topologies and uncover new insights into functional organization patterns. This allows us to associate brain functional connectivity (FC) patterns of conservative signals with well-known functional segregation and integration properties. Our findings align with recent neuroscience research, suggesting that our approach may offer a promising pathway for characterizing the higher-order brain functional connectivities.

Stability of Graph Convolutional Neural Networks through the lens of small perturbation analysis

In this work, we study the problem of stability of Graph Convolutional Neural Networks (GCNs) under random small perturbations in the underlying graph topology, i.e. under a limited number of insertions or deletions of edges. We derive a novel bound on the expected difference between the outputs of unperturbed and perturbed GCNs. The proposed bound explicitly depends on the magnitude of the perturbation of the eigenpairs of the Laplacian matrix, and the perturbation explicitly depends on which edges are inserted or deleted. Then, we provide a quantitative characterization of the effect of perturbing specific edges on the stability of the network. We leverage tools from small perturbation analysis to express the bounds in closed, albeit approximate, form, in order to enhance interpretability of the results, without the need to compute any perturbed shift operator. Finally, we numerically evaluate the effectiveness of the proposed bound.

Learning Multi-Frequency Partial Correlation Graphs

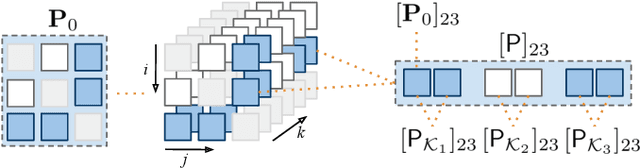
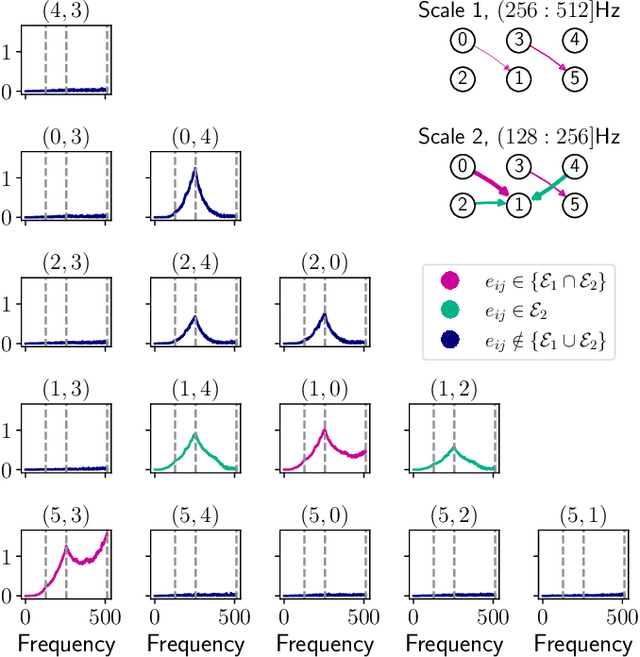
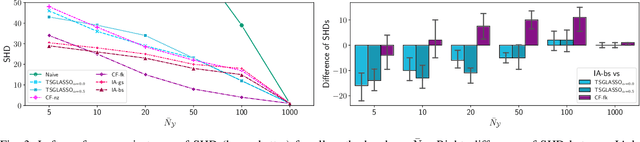
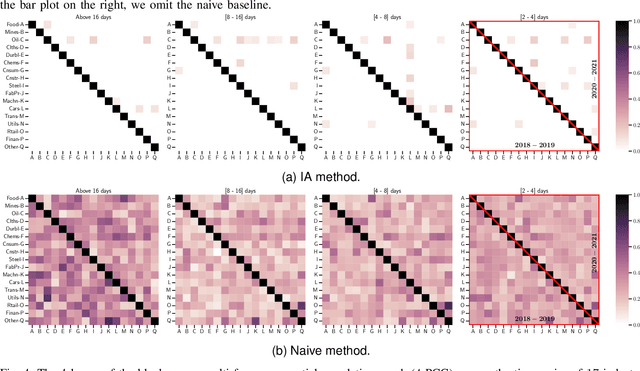
Despite the large research effort devoted to learning dependencies between time series, the state of the art still faces a major limitation: existing methods learn partial correlations but fail to discriminate across distinct frequency bands. Motivated by many applications in which this differentiation is pivotal, we overcome this limitation by learning a block-sparse, frequency-dependent, partial correlation graph, in which layers correspond to different frequency bands, and partial correlations can occur over just a few layers. To this aim, we formulate and solve two nonconvex learning problems: the first has a closed-form solution and is suitable when there is prior knowledge about the number of partial correlations; the second hinges on an iterative solution based on successive convex approximation, and is effective for the general case where no prior knowledge is available. Numerical results on synthetic data show that the proposed methods outperform the current state of the art. Finally, the analysis of financial time series confirms that partial correlations exist only within a few frequency bands, underscoring how our methods enable the gaining of valuable insights that would be undetected without discriminating along the frequency domain.

Generalized Simplicial Attention Neural Networks

The aim of this work is to introduce Generalized Simplicial Attention Neural Networks (GSANs), i.e., novel neural architectures designed to process data defined on simplicial complexes using masked self-attentional layers. Hinging on topological signal processing principles, we devise a series of self-attention schemes capable of processing data components defined at different simplicial orders, such as nodes, edges, triangles, and beyond. These schemes learn how to weight the neighborhoods of the given topological domain in a task-oriented fashion, leveraging the interplay among simplices of different orders through the Dirac operator and its Dirac decomposition. We also theoretically establish that GSANs are permutation equivariant and simplicial-aware. Finally, we illustrate how our approach compares favorably with other methods when applied to several (inductive and transductive) tasks such as trajectory prediction, missing data imputation, graph classification, and simplex prediction.

Topological Signal Processing over Weighted Simplicial Complexes

Weighing the topological domain over which data can be represented and analysed is a key strategy in many signal processing and machine learning applications, enabling the extraction and exploitation of meaningful data features and their (higher order) relationships. Our goal in this paper is to present topological signal processing tools for weighted simplicial complexes. Specifically, relying on the weighted Hodge Laplacian theory, we propose efficient strategies to jointly learn the weights of the complex and the filters for the solenoidal, irrotational and harmonic components of the signals defined over the complex. We numerically asses the effectiveness of the proposed procedures.

Cell Attention Networks

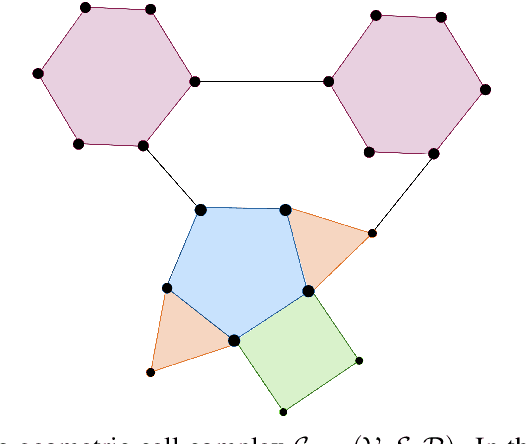
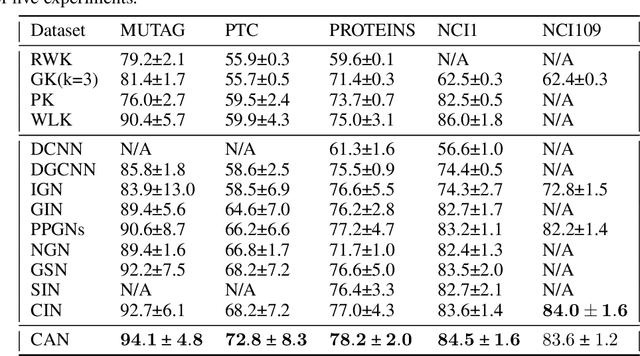
Since their introduction, graph attention networks achieved outstanding results in graph representation learning tasks. However, these networks consider only pairwise relationships among nodes and then they are not able to fully exploit higher-order interactions present in many real world data-sets. In this paper, we introduce Cell Attention Networks (CANs), a neural architecture operating on data defined over the vertices of a graph, representing the graph as the 1-skeleton of a cell complex introduced to capture higher order interactions. In particular, we exploit the lower and upper neighborhoods, as encoded in the cell complex, to design two independent masked self-attention mechanisms, thus generalizing the conventional graph attention strategy. The approach used in CANs is hierarchical and it incorporates the following steps: i) a lifting algorithm that learns {\it edge features} from {\it node features}; ii) a cell attention mechanism to find the optimal combination of edge features over both lower and upper neighbors; iii) a hierarchical {\it edge pooling} mechanism to extract a compact meaningful set of features. The experimental results show that CAN is a low complexity strategy that compares favorably with state of the art results on graph-based learning tasks.

Topological Signal Representation and Processing over Cell Complexes

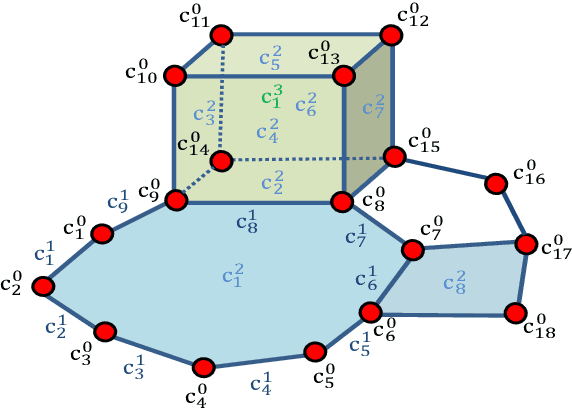
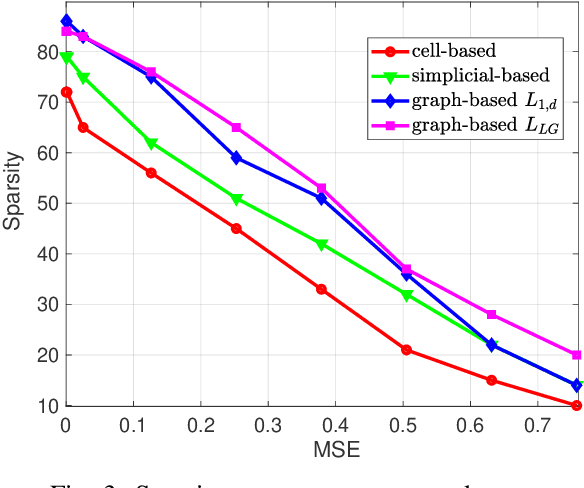
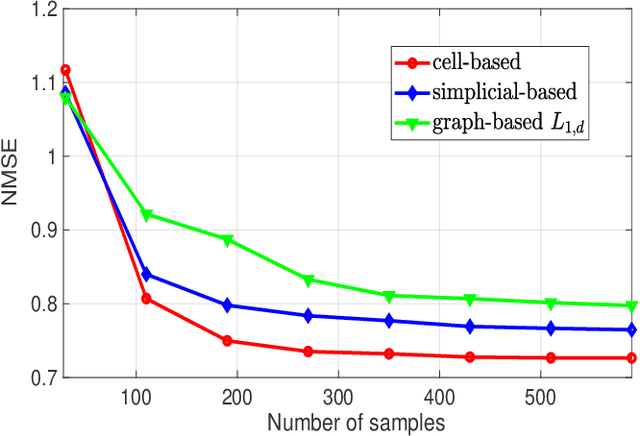
Topological Signal Processing (TSP) over simplicial complexes is a framework that has been recently proposed, as a generalization of graph signal processing (GSP), aimed to analyze signals defined over sets of any order (i.e. not only vertices of a graph) and to capture relations of any order present in the observed data. Our goal in this paper is to extend the TSP framework to deal with signals defined over cell complexes, i.e. topological spaces that are not constrained to satisfy the inclusion property of simplicial complexes, namely the condition that, if a set belongs to the complex, then all its subsets belong to the complex as well. We start showing how to translate the algebraic topological tools to deal with signals defined over cell complexes and then we propose a method to infer the structure of the cell complex from data. Then, we address the filtering problem over cell complexes and we provide the theoretical conditions under which the independent filtering of the solenoidal and irrotational components of edge signals brings a performance improvement with respect to a common filtering strategy. Furthermore, we propose a distributed strategy to filter the harmonic signals with the aim of retrieving the sparsest representation of the harmonic components. Finally, we quantify the advantages of using cell complexes instead of simplicial complexes, in terms of the sparsity/accuracy trade-off and of the signal recovery accuracy from sparse samples, using both simulated and real flows measured on data traffic and transportation networks.

Topological Signal Processing over Cell Complexes

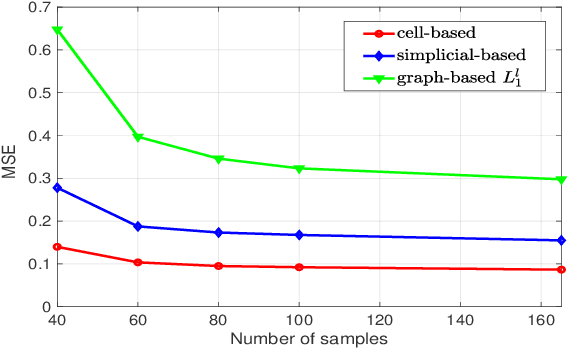
The Topological Signal Processing (TSP) framework has been recently developed to analyze signals defined over simplicial complexes, i.e. topological spaces represented by finite sets of elements that are closed under inclusion of subsets [1]. However, the same inclusion property represents sometimes a too rigid assumption that prevents the application of simplicial complexes to many cases of interest. The goal of this paper is to extend TSP to the analysis of signals defined over cell complexes, which represent a generalization of simplicial complexes, as they are not restricted to satisfy the inclusion property. In particular, the richer topological structure of cell complexes enables them to reveal cycles of any order, as representative of data features. We propose an efficient method to infer the topology of cell complexes from data by showing how their use enables sparser edge signal representations than simplicial-based methods. Furthermore, we show how to design optimal finite impulse response (FIR) filters operating on solenoidal and irrotational signals in order to minimize the approximation error with respect to the desired spectral masks.