Topological Signal Representation and Processing over Cell Complexes

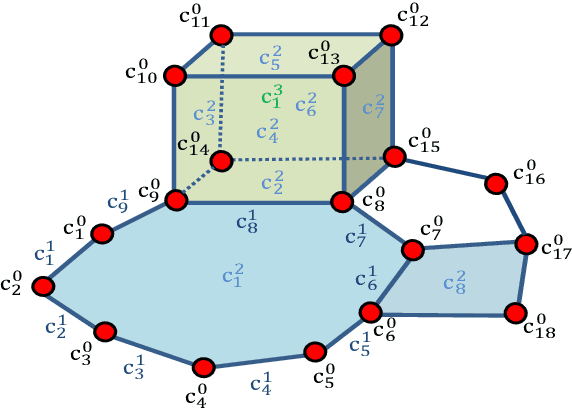
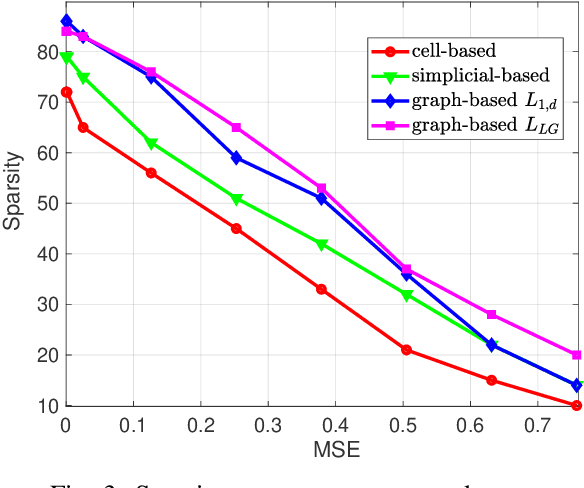
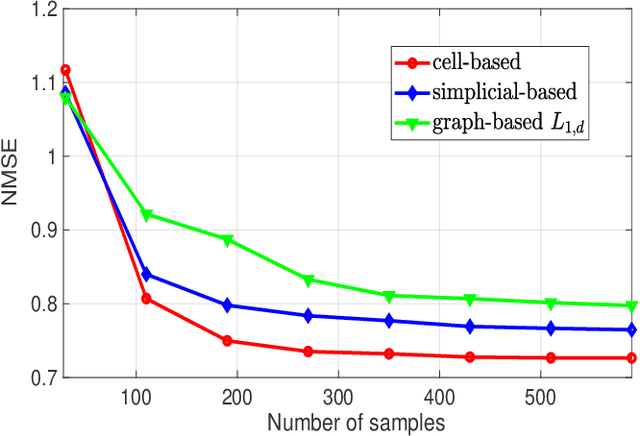
Topological Signal Processing (TSP) over simplicial complexes is a framework that has been recently proposed, as a generalization of graph signal processing (GSP), aimed to analyze signals defined over sets of any order (i.e. not only vertices of a graph) and to capture relations of any order present in the observed data. Our goal in this paper is to extend the TSP framework to deal with signals defined over cell complexes, i.e. topological spaces that are not constrained to satisfy the inclusion property of simplicial complexes, namely the condition that, if a set belongs to the complex, then all its subsets belong to the complex as well. We start showing how to translate the algebraic topological tools to deal with signals defined over cell complexes and then we propose a method to infer the structure of the cell complex from data. Then, we address the filtering problem over cell complexes and we provide the theoretical conditions under which the independent filtering of the solenoidal and irrotational components of edge signals brings a performance improvement with respect to a common filtering strategy. Furthermore, we propose a distributed strategy to filter the harmonic signals with the aim of retrieving the sparsest representation of the harmonic components. Finally, we quantify the advantages of using cell complexes instead of simplicial complexes, in terms of the sparsity/accuracy trade-off and of the signal recovery accuracy from sparse samples, using both simulated and real flows measured on data traffic and transportation networks.