Topological Signal Processing over Weighted Simplicial Complexes
Paper and Code
Feb 16, 2023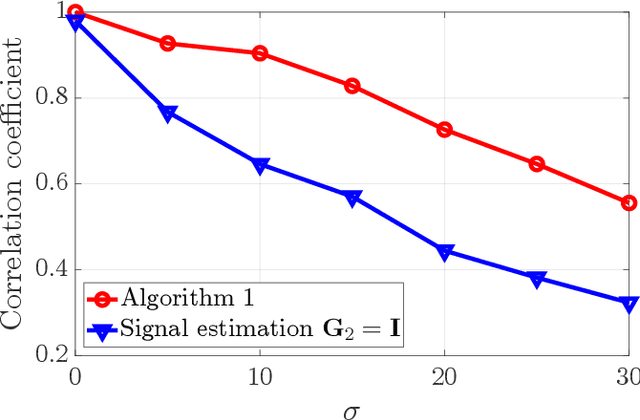
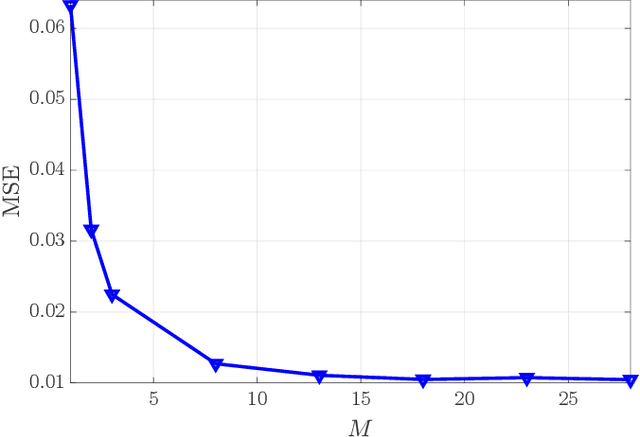
Weighing the topological domain over which data can be represented and analysed is a key strategy in many signal processing and machine learning applications, enabling the extraction and exploitation of meaningful data features and their (higher order) relationships. Our goal in this paper is to present topological signal processing tools for weighted simplicial complexes. Specifically, relying on the weighted Hodge Laplacian theory, we propose efficient strategies to jointly learn the weights of the complex and the filters for the solenoidal, irrotational and harmonic components of the signals defined over the complex. We numerically asses the effectiveness of the proposed procedures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge