Spectral Diffusion Models on the Sphere

Diffusion models provide a principled framework for generative modeling via stochastic differential equations and time-reversed dynamics. Extending spectral diffusion approaches to spherical data, however, raises nontrivial geometric and stochastic issues that are absent in the Euclidean setting. In this work, we develop a diffusion modeling framework defined directly on finite-dimensional spherical harmonic representations of real-valued functions on the sphere. We show that the spherical discrete Fourier transform maps spatial Brownian motion to a constrained Gaussian process in the frequency domain with deterministic, generally non-isotropic covariance. This induces modified forward and reverse-time stochastic differential equations in the spectral domain. As a consequence, spatial and spectral score matching objectives are no longer equivalent, even in the band-limited setting, and the frequency-domain formulation introduces a geometry-dependent inductive bias. We derive the corresponding diffusion equations and characterize the induced noise covariance.

Statistical Foundations of DIME: Risk Estimation for Practical Index Selection

High-dimensional dense embeddings have become central to modern Information Retrieval, but many dimensions are noisy or redundant. Recently proposed DIME (Dimension IMportance Estimation), provides query-dependent scores to identify informative components of embeddings. DIME relies on a costly grid search to select a priori a dimensionality for all the query corpus's embeddings. Our work provides a statistically grounded criterion that directly identifies the optimal set of dimensions for each query at inference time. Experiments confirm achieving parity of effectiveness and reduces embedding size by an average of $\sim50\%$ across different models and datasets at inference time.

Federated GNNs for EEG-Based Stroke Assessment

Machine learning (ML) has the potential to become an essential tool in supporting clinical decision-making processes, offering enhanced diagnostic capabilities and personalized treatment plans. However, outsourcing medical records to train ML models using patient data raises legal, privacy, and security concerns. Federated learning has emerged as a promising paradigm for collaborative ML, meeting healthcare institutions' requirements for robust models without sharing sensitive data and compromising patient privacy. This study proposes a novel method that combines federated learning (FL) and Graph Neural Networks (GNNs) to predict stroke severity using electroencephalography (EEG) signals across multiple medical institutions. Our approach enables multiple hospitals to jointly train a shared GNN model on their local EEG data without exchanging patient information. Specifically, we address a regression problem by predicting the National Institutes of Health Stroke Scale (NIHSS), a key indicator of stroke severity. The proposed model leverages a masked self-attention mechanism to capture salient brain connectivity patterns and employs EdgeSHAP to provide post-hoc explanations of the neurological states after a stroke. We evaluated our method on EEG recordings from four institutions, achieving a mean absolute error (MAE) of 3.23 in predicting NIHSS, close to the average error made by human experts (MAE $\approx$ 3.0). This demonstrates the method's effectiveness in providing accurate and explainable predictions while maintaining data privacy.

Energy Trees: Regression and Classification With Structured and Mixed-Type Covariates

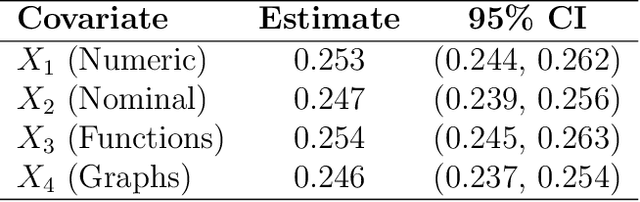
The continuous growth of data complexity requires methods and models that adequately account for non-trivial structures, as any simplification may induce loss of information. Many analytical tools have been introduced to work with complex data objects in their original form, but such tools can typically deal with single-type variables only. In this work, we propose Energy Trees as a model for regression and classification tasks where covariates are potentially both structured and of different types. Energy Trees incorporate Energy Statistics to generalize Conditional Trees, from which they inherit statistically sound foundations, interpretability, scale invariance, and lack of distributional assumptions. We focus on functions and graphs as structured covariates and we show how the model can be easily adapted to work with almost any other type of variable. Through an extensive simulation study, we highlight the good performance of our proposal in terms of variable selection and robustness to overfitting. Finally, we validate the model's predictive ability through two empirical analyses with human biological data.

Reprogramming FairGANs with Variational Auto-Encoders: A New Transfer Learning Model

Fairness-aware GANs (FairGANs) exploit the mechanisms of Generative Adversarial Networks (GANs) to impose fairness on the generated data, freeing them from both disparate impact and disparate treatment. Given the model's advantages and performance, we introduce a novel learning framework to transfer a pre-trained FairGAN to other tasks. This reprogramming process has the goal of maintaining the FairGAN's main targets of data utility, classification utility, and data fairness, while widening its applicability and ease of use. In this paper we present the technical extensions required to adapt the original architecture to this new framework (and in particular the use of Variational Auto-Encoders), and discuss the benefits, trade-offs, and limitations of the new model.

Supervised Learning with Indefinite Topological Kernels

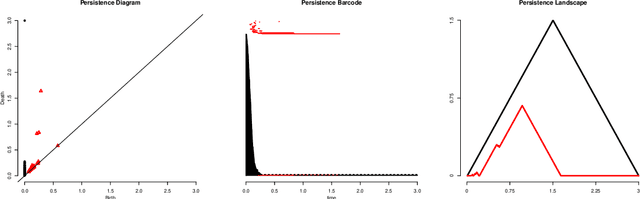
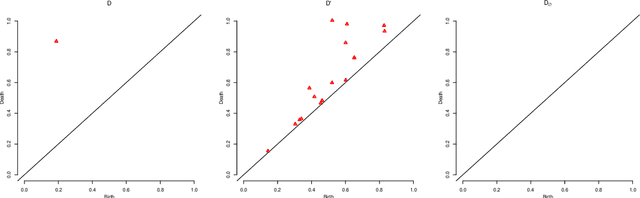
Topological Data Analysis (TDA) is a recent and growing branch of statistics devoted to the study of the shape of the data. In this work we investigate the predictive power of TDA in the context of supervised learning. Since topological summaries, most noticeably the Persistence Diagram, are typically defined in complex spaces, we adopt a kernel approach to translate them into more familiar vector spaces. We define a topological exponential kernel, we characterize it, and we show that, despite not being positive semi-definite, it can be successfully used in regression and classification tasks.

Persistence Flamelets: multiscale Persistent Homology for kernel density exploration

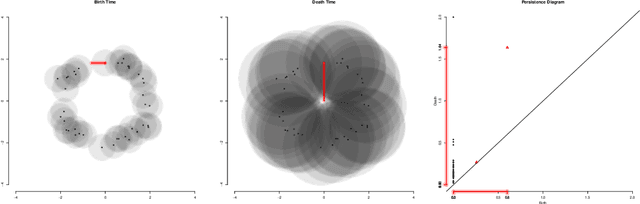
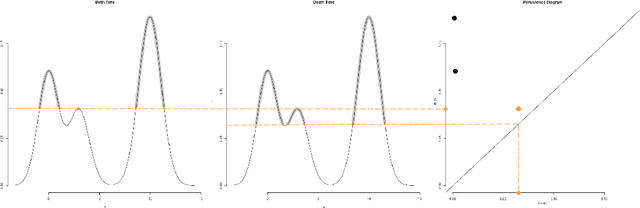
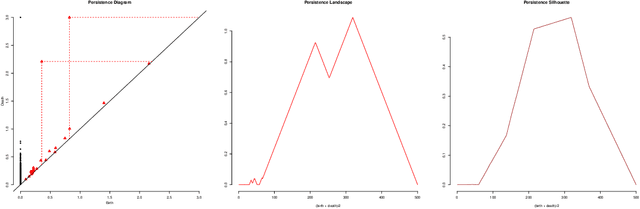
In recent years there has been noticeable interest in the study of the "shape of data". Among the many ways a "shape" could be defined, topology is the most general one, as it describes an object in terms of its connectivity structure: connected components (topological features of dimension 0), cycles (features of dimension 1) and so on. There is a growing number of techniques, generally denoted as Topological Data Analysis, aimed at estimating topological invariants of a fixed object; when we allow this object to change, however, little has been done to investigate the evolution in its topology. In this work we define the Persistence Flamelets, a multiscale version of one of the most popular tool in TDA, the Persistence Landscape. We examine its theoretical properties and we show how it could be used to gain insights on KDEs bandwidth parameter.