Energy Trees: Regression and Classification With Structured and Mixed-Type Covariates

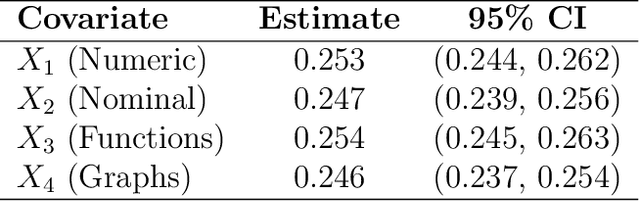
The continuous growth of data complexity requires methods and models that adequately account for non-trivial structures, as any simplification may induce loss of information. Many analytical tools have been introduced to work with complex data objects in their original form, but such tools can typically deal with single-type variables only. In this work, we propose Energy Trees as a model for regression and classification tasks where covariates are potentially both structured and of different types. Energy Trees incorporate Energy Statistics to generalize Conditional Trees, from which they inherit statistically sound foundations, interpretability, scale invariance, and lack of distributional assumptions. We focus on functions and graphs as structured covariates and we show how the model can be easily adapted to work with almost any other type of variable. Through an extensive simulation study, we highlight the good performance of our proposal in terms of variable selection and robustness to overfitting. Finally, we validate the model's predictive ability through two empirical analyses with human biological data.

Supervised Learning with Indefinite Topological Kernels

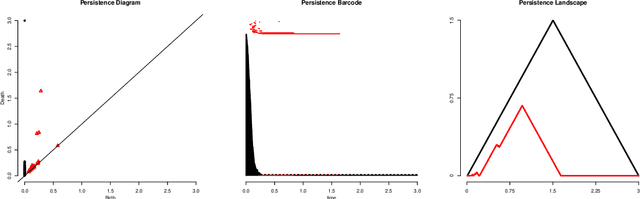
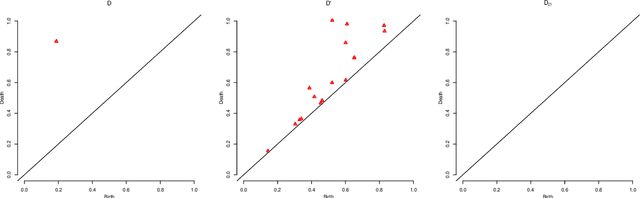
Topological Data Analysis (TDA) is a recent and growing branch of statistics devoted to the study of the shape of the data. In this work we investigate the predictive power of TDA in the context of supervised learning. Since topological summaries, most noticeably the Persistence Diagram, are typically defined in complex spaces, we adopt a kernel approach to translate them into more familiar vector spaces. We define a topological exponential kernel, we characterize it, and we show that, despite not being positive semi-definite, it can be successfully used in regression and classification tasks.

Persistence Flamelets: multiscale Persistent Homology for kernel density exploration

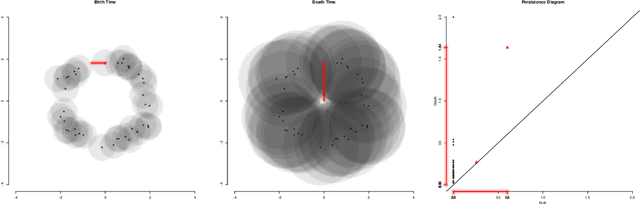
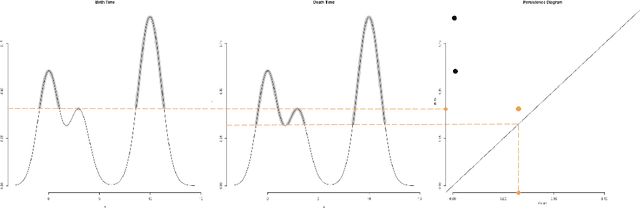
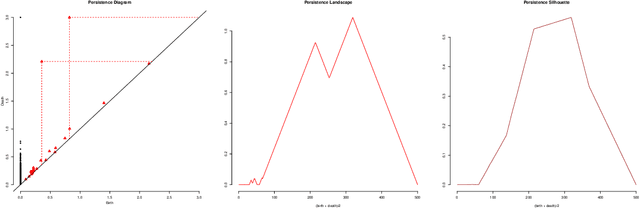
In recent years there has been noticeable interest in the study of the "shape of data". Among the many ways a "shape" could be defined, topology is the most general one, as it describes an object in terms of its connectivity structure: connected components (topological features of dimension 0), cycles (features of dimension 1) and so on. There is a growing number of techniques, generally denoted as Topological Data Analysis, aimed at estimating topological invariants of a fixed object; when we allow this object to change, however, little has been done to investigate the evolution in its topology. In this work we define the Persistence Flamelets, a multiscale version of one of the most popular tool in TDA, the Persistence Landscape. We examine its theoretical properties and we show how it could be used to gain insights on KDEs bandwidth parameter.