Private Heavy Hitters and Range Queries in the Shuffled Model

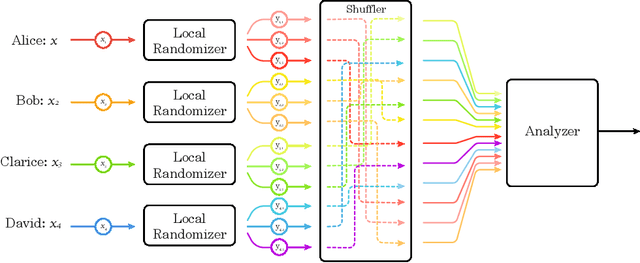
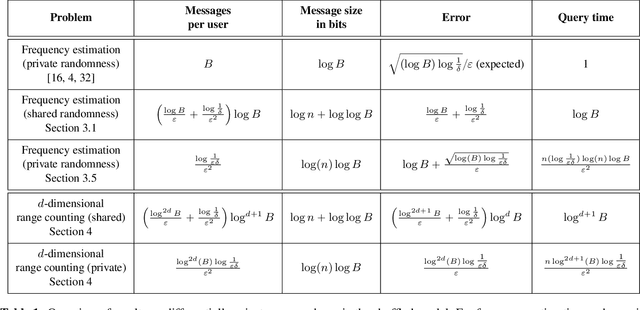
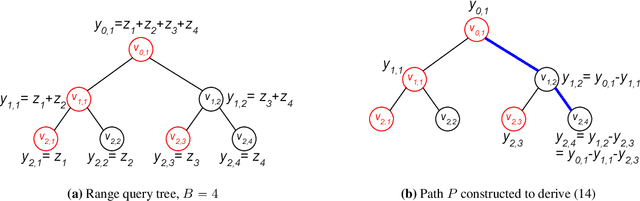
An exciting new development in differential privacy is the shuffled model, which makes it possible to circumvent the large error lower bounds that are typically incurred in the local model, while relying on much weaker trust assumptions than in the central model. In this work, we study two basic statistical problems, namely, heavy hitters and $d$-dimensional range counting queries, in the shuffled model of privacy. For both problems we devise algorithms with polylogarithmic communication per user and polylogarithmic error; a consequence is an algorithm for approximating the median with similar communication and error. These bounds significantly improve on what is possible in the local model of differential privacy, where the error must provably grow polynomially with the number of users.