BalanceKV: KV Cache Compression through Discrepancy Theory

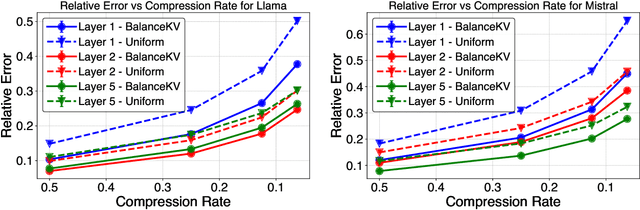
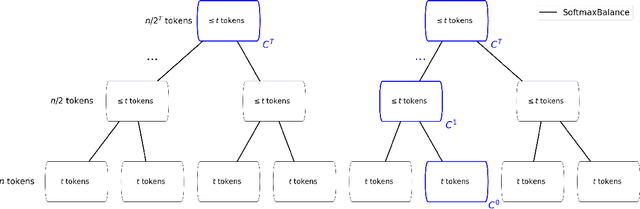
Large language models (LLMs) have achieved impressive success, but their high memory requirements present challenges for long-context token generation. The memory complexity of long-context LLMs is primarily due to the need to store Key-Value (KV) embeddings in their KV cache. We present BalanceKV, a KV cache compression method based on geometric sampling process stemming from Banaszczyk's vector balancing theory, which introduces dependencies informed by the geometry of keys and value tokens, and improves precision. BalanceKV offers both theoretically proven and empirically validated performance improvements over existing methods.

Improved Linear Embeddings via Lagrange Duality

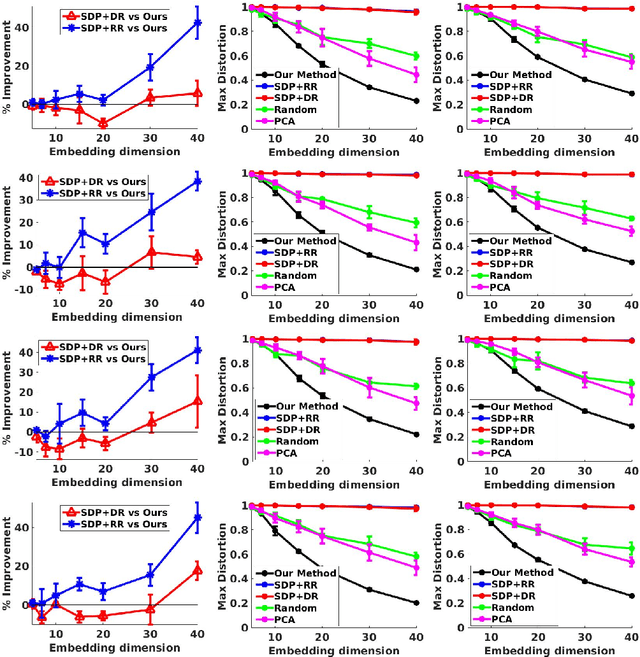
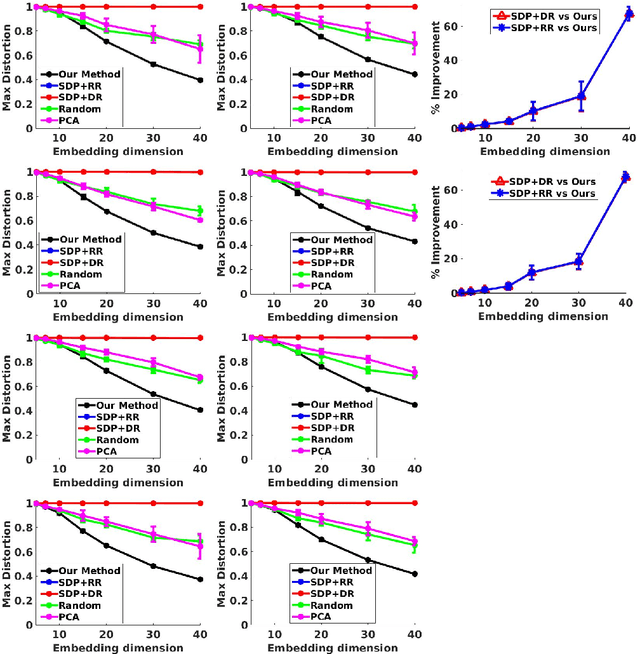
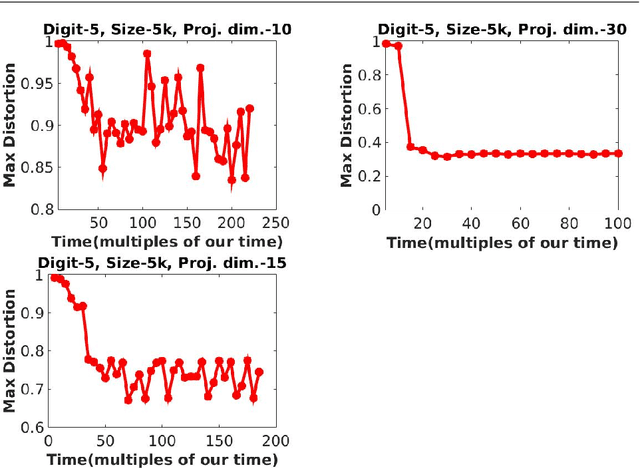
Near isometric orthogonal embeddings to lower dimensions are a fundamental tool in data science and machine learning. In this paper, we present the construction of such embeddings that minimizes the maximum distortion for a given set of points. We formulate the problem as a non convex constrained optimization problem. We first construct a primal relaxation and then use the theory of Lagrange duality to create dual relaxation. We also suggest a polynomial time algorithm based on the theory of convex optimization to solve the dual relaxation provably. We provide a theoretical upper bound on the approximation guarantees for our algorithm, which depends only on the spectral properties of the dataset. We experimentally demonstrate the superiority of our algorithm compared to baselines in terms of the scalability and the ability to achieve lower distortion.

Deep-Learnt Classification of Light Curves

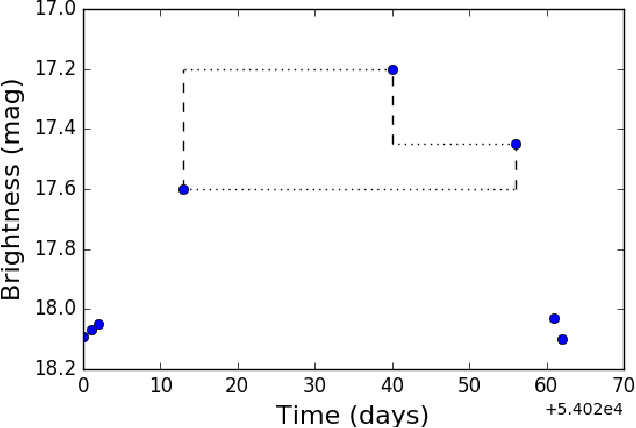
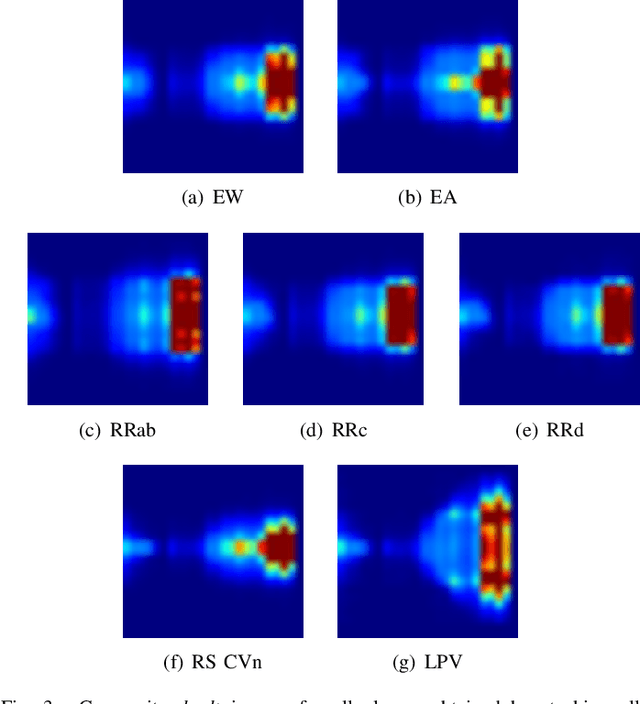
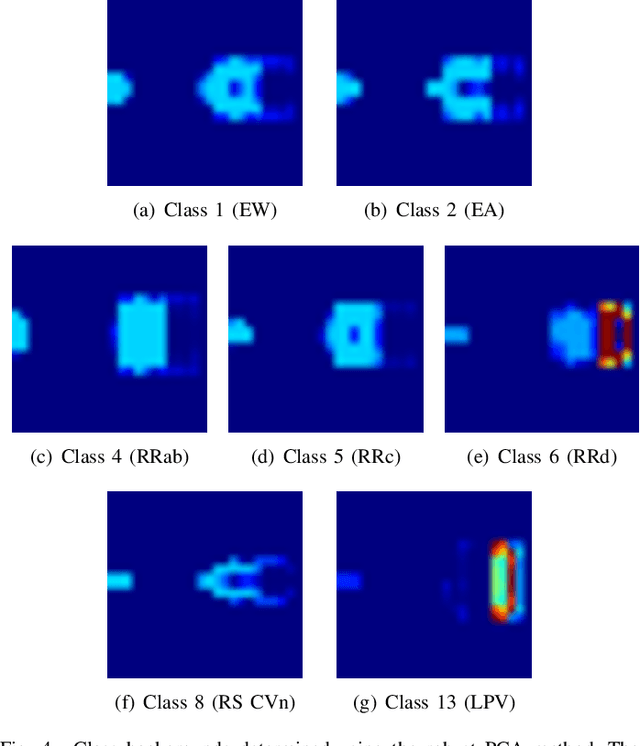
Astronomy light curves are sparse, gappy, and heteroscedastic. As a result standard time series methods regularly used for financial and similar datasets are of little help and astronomers are usually left to their own instruments and techniques to classify light curves. A common approach is to derive statistical features from the time series and to use machine learning methods, generally supervised, to separate objects into a few of the standard classes. In this work, we transform the time series to two-dimensional light curve representations in order to classify them using modern deep learning techniques. In particular, we show that convolutional neural networks based classifiers work well for broad characterization and classification. We use labeled datasets of periodic variables from CRTS survey and show how this opens doors for a quick classification of diverse classes with several possible exciting extensions.

Deep Neural Networks for HDR imaging

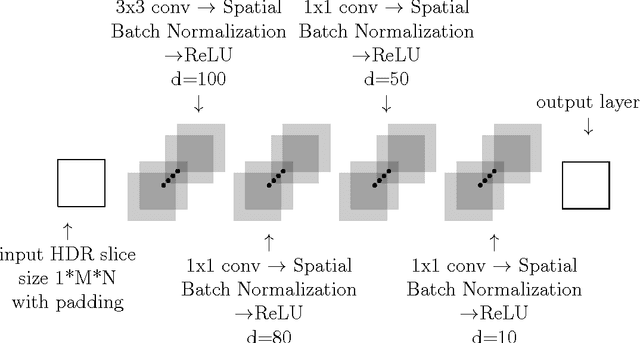
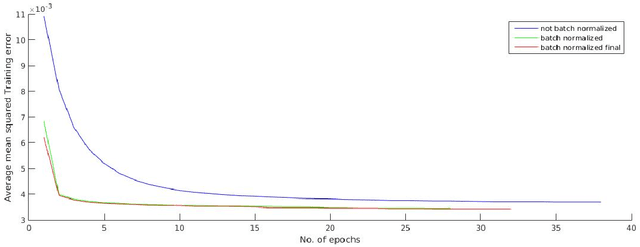
We propose novel methods of solving two tasks using Convolutional Neural Networks, firstly the task of generating HDR map of a static scene using differently exposed LDR images of the scene captured using conventional cameras and secondly the task of finding an optimal tone mapping operator that would give a better score on the TMQI metric compared to the existing methods. We quantitatively show the performance of our networks and illustrate the cases where our networks performs good as well as bad.