Improved Linear Embeddings via Lagrange Duality
Paper and Code
Dec 14, 2017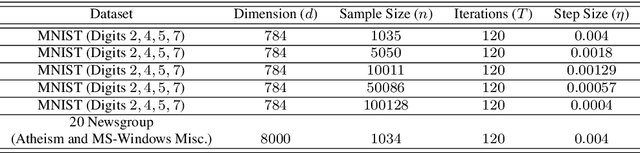
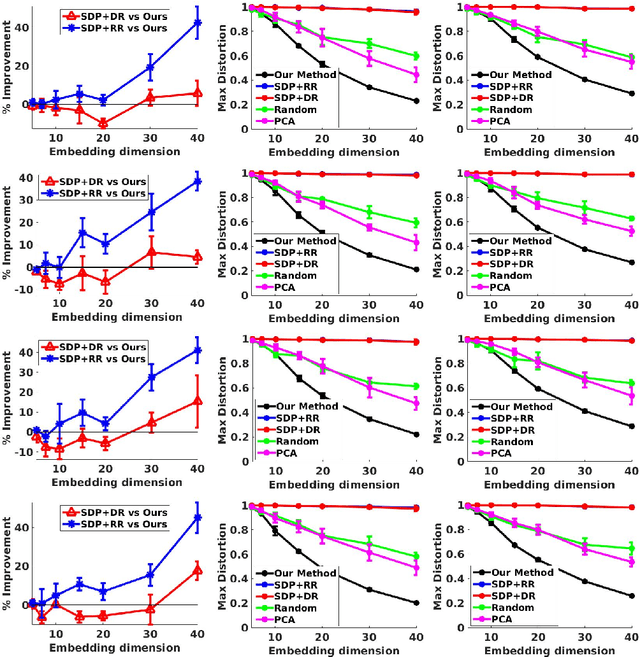
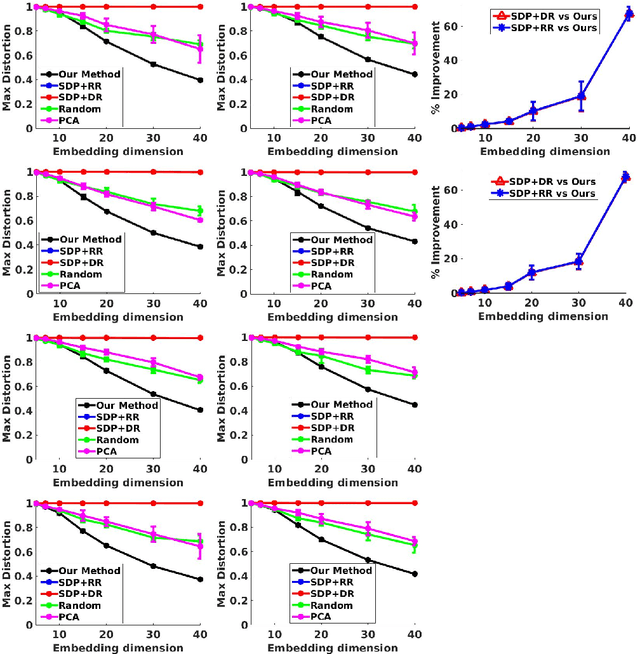
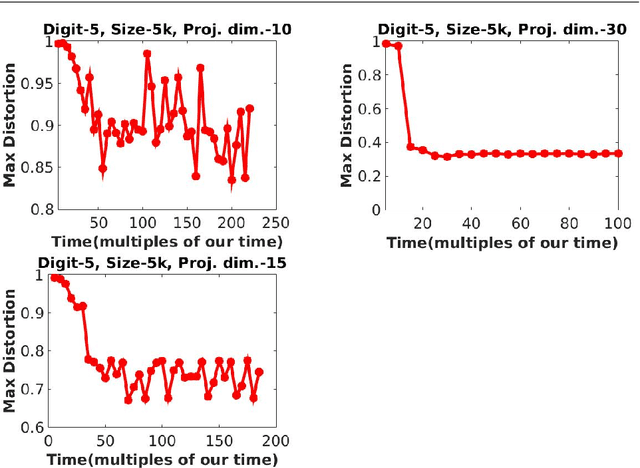
Near isometric orthogonal embeddings to lower dimensions are a fundamental tool in data science and machine learning. In this paper, we present the construction of such embeddings that minimizes the maximum distortion for a given set of points. We formulate the problem as a non convex constrained optimization problem. We first construct a primal relaxation and then use the theory of Lagrange duality to create dual relaxation. We also suggest a polynomial time algorithm based on the theory of convex optimization to solve the dual relaxation provably. We provide a theoretical upper bound on the approximation guarantees for our algorithm, which depends only on the spectral properties of the dataset. We experimentally demonstrate the superiority of our algorithm compared to baselines in terms of the scalability and the ability to achieve lower distortion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge