Near Optimal Reconstruction of Spherical Harmonic Expansions
Paper and Code
Feb 25, 2022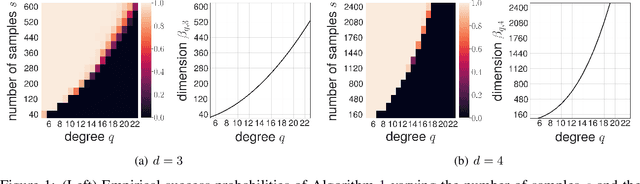
We propose an algorithm for robust recovery of the spherical harmonic expansion of functions defined on the d-dimensional unit sphere $\mathbb{S}^{d-1}$ using a near-optimal number of function evaluations. We show that for any $f \in L^2(\mathbb{S}^{d-1})$, the number of evaluations of $f$ needed to recover its degree-$q$ spherical harmonic expansion equals the dimension of the space of spherical harmonics of degree at most $q$ up to a logarithmic factor. Moreover, we develop a simple yet efficient algorithm to recover degree-$q$ expansion of $f$ by only evaluating the function on uniformly sampled points on $\mathbb{S}^{d-1}$. Our algorithm is based on the connections between spherical harmonics and Gegenbauer polynomials and leverage score sampling methods. Unlike the prior results on fast spherical harmonic transform, our proposed algorithm works efficiently using a nearly optimal number of samples in any dimension d. We further illustrate the empirical performance of our algorithm on numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge