Majid Daliri
New York University
CombiGraph-Vis: A Curated Multimodal Olympiad Benchmark for Discrete Mathematical Reasoning
Oct 31, 2025Abstract:State-of-the-art (SOTA) LLMs have progressed from struggling on proof-based Olympiad problems to solving most of the IMO 2025 problems, with leading systems reportedly handling 5 of 6 problems. Given this progress, we assess how well these models can grade proofs: detecting errors, judging their severity, and assigning fair scores beyond binary correctness. We study proof-analysis capabilities using a corpus of 90 Gemini 2.5 Pro-generated solutions that we grade on a 1-4 scale with detailed error annotations, and on MathArena solution sets for IMO/USAMO 2025 scored on a 0-7 scale. Our analysis shows that models can reliably flag incorrect (including subtly incorrect) solutions but exhibit calibration gaps in how partial credit is assigned. To address this, we introduce agentic workflows that extract and analyze reference solutions and automatically derive problem-specific rubrics for a multi-step grading process. We instantiate and compare different design choices for the grading workflows, and evaluate their trade-offs. Across our annotated corpus and MathArena, our proposed workflows achieve higher agreement with human grades and more consistent handling of partial credit across metrics. We release all code, data, and prompts/logs to facilitate future research.
ATLAS: Learning to Optimally Memorize the Context at Test Time
May 29, 2025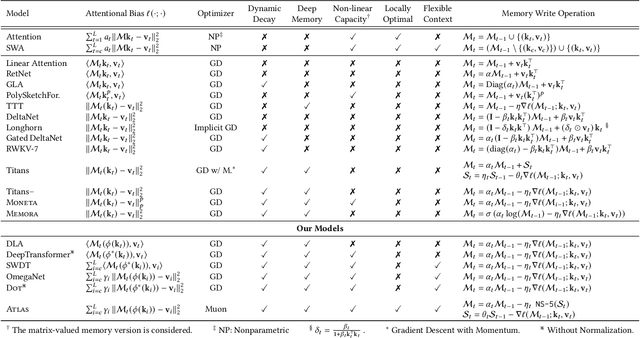
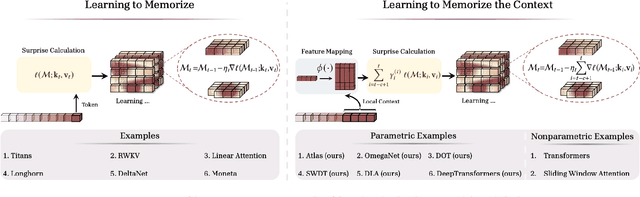
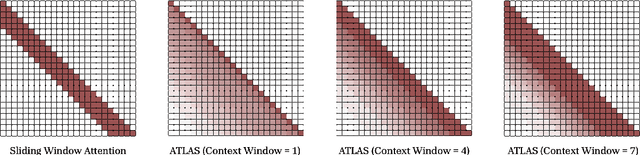
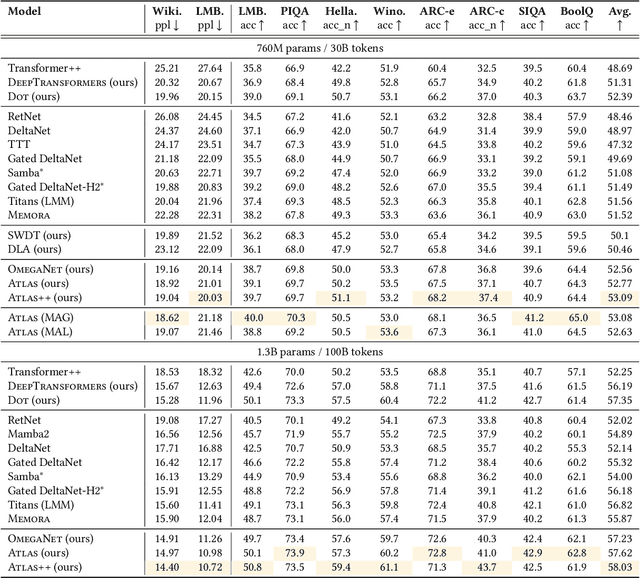
Abstract:Transformers have been established as the most popular backbones in sequence modeling, mainly due to their effectiveness in in-context retrieval tasks and the ability to learn at scale. Their quadratic memory and time complexity, however, bound their applicability in longer sequences and so has motivated researchers to explore effective alternative architectures such as modern recurrent neural networks (a.k.a long-term recurrent memory module). Despite their recent success in diverse downstream tasks, they struggle in tasks that requires long context understanding and extrapolation to longer sequences. We observe that these shortcomings come from three disjoint aspects in their design: (1) limited memory capacity that is bounded by the architecture of memory and feature mapping of the input; (2) online nature of update, i.e., optimizing the memory only with respect to the last input; and (3) less expressive management of their fixed-size memory. To enhance all these three aspects, we present ATLAS, a long-term memory module with high capacity that learns to memorize the context by optimizing the memory based on the current and past tokens, overcoming the online nature of long-term memory models. Building on this insight, we present a new family of Transformer-like architectures, called DeepTransformers, that are strict generalizations of the original Transformer architecture. Our experimental results on language modeling, common-sense reasoning, recall-intensive, and long-context understanding tasks show that ATLAS surpasses the performance of Transformers and recent linear recurrent models. ATLAS further improves the long context performance of Titans, achieving +80\% accuracy in 10M context length of BABILong benchmark.
TurboQuant: Online Vector Quantization with Near-optimal Distortion Rate
Apr 28, 2025



Abstract:Vector quantization, a problem rooted in Shannon's source coding theory, aims to quantize high-dimensional Euclidean vectors while minimizing distortion in their geometric structure. We propose TurboQuant to address both mean-squared error (MSE) and inner product distortion, overcoming limitations of existing methods that fail to achieve optimal distortion rates. Our data-oblivious algorithms, suitable for online applications, achieve near-optimal distortion rates (within a small constant factor) across all bit-widths and dimensions. TurboQuant achieves this by randomly rotating input vectors, inducing a concentrated Beta distribution on coordinates, and leveraging the near-independence property of distinct coordinates in high dimensions to simply apply optimal scalar quantizers per each coordinate. Recognizing that MSE-optimal quantizers introduce bias in inner product estimation, we propose a two-stage approach: applying an MSE quantizer followed by a 1-bit Quantized JL (QJL) transform on the residual, resulting in an unbiased inner product quantizer. We also provide a formal proof of the information-theoretic lower bounds on best achievable distortion rate by any vector quantizer, demonstrating that TurboQuant closely matches these bounds, differing only by a small constant ($\approx 2.7$) factor. Experimental results validate our theoretical findings, showing that for KV cache quantization, we achieve absolute quality neutrality with 3.5 bits per channel and marginal quality degradation with 2.5 bits per channel. Furthermore, in nearest neighbor search tasks, our method outperforms existing product quantization techniques in recall while reducing indexing time to virtually zero.
Brains vs. Bytes: Evaluating LLM Proficiency in Olympiad Mathematics
Apr 01, 2025Abstract:Recent advancements in large language models (LLMs) have shown impressive progress in mathematical reasoning tasks. However, current evaluation benchmarks predominantly focus on the accuracy of final answers, often overlooking the logical rigor crucial for mathematical problem-solving. The claim that state-of-the-art LLMs can solve Math Olympiad-level problems requires closer examination. To explore this, we conducted both qualitative and quantitative human evaluations of proofs generated by LLMs, and developed a schema for automatically assessing their reasoning capabilities. Our study reveals that current LLMs fall significantly short of solving challenging Olympiad-level problems and frequently fail to distinguish correct mathematical reasoning from clearly flawed solutions. We also found that occasional correct final answers provided by LLMs often result from pattern recognition or heuristic shortcuts rather than genuine mathematical reasoning. These findings underscore the substantial gap between LLM performance and human expertise in advanced mathematical reasoning and highlight the importance of developing benchmarks that prioritize the rigor and coherence of mathematical arguments rather than merely the correctness of final answers.
Matrix Product Sketching via Coordinated Sampling
Jan 29, 2025



Abstract:We revisit the well-studied problem of approximating a matrix product, $\mathbf{A}^T\mathbf{B}$, based on small space sketches $\mathcal{S}(\mathbf{A})$ and $\mathcal{S}(\mathbf{B})$ of $\mathbf{A} \in \R^{n \times d}$ and $\mathbf{B}\in \R^{n \times m}$. We are interested in the setting where the sketches must be computed independently of each other, except for the use of a shared random seed. We prove that, when $\mathbf{A}$ and $\mathbf{B}$ are sparse, methods based on \emph{coordinated random sampling} can outperform classical linear sketching approaches, like Johnson-Lindenstrauss Projection or CountSketch. For example, to obtain Frobenius norm error $\epsilon\|\mathbf{A}\|_F\|\mathbf{B}\|_F$, coordinated sampling requires sketches of size $O(s/\epsilon^2)$ when $\mathbf{A}$ and $\mathbf{B}$ have at most $s \leq d,m$ non-zeros per row. In contrast, linear sketching leads to sketches of size $O(d/\epsilon^2)$ and $O(m/\epsilon^2)$ for $\mathbf{A}$ and $\mathbf{B}$. We empirically evaluate our approach on two applications: 1) distributed linear regression in databases, a problem motivated by tasks like dataset discovery and augmentation, and 2) approximating attention matrices in transformer-based language models. In both cases, our sampling algorithms yield an order of magnitude improvement over linear sketching.
Unlocking the Theory Behind Scaling 1-Bit Neural Networks
Nov 03, 2024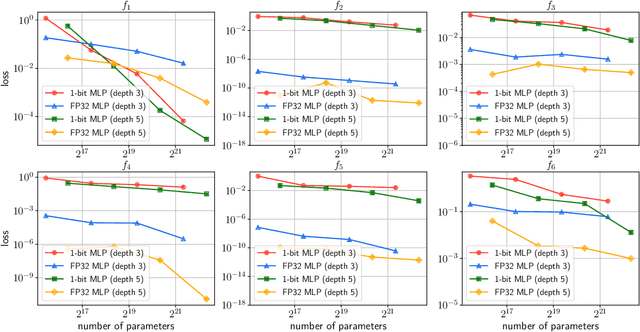
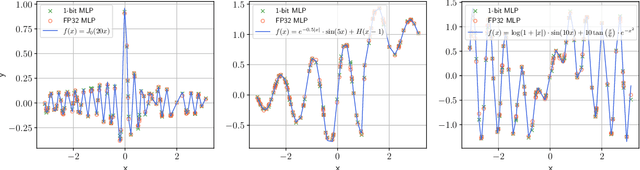
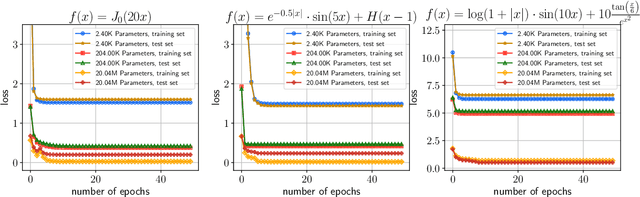
Abstract:Recently, 1-bit Large Language Models (LLMs) have emerged, showcasing an impressive combination of efficiency and performance that rivals traditional LLMs. Research by Wang et al. (2023); Ma et al. (2024) indicates that the performance of these 1-bit LLMs progressively improves as the number of parameters increases, hinting at the potential existence of a Scaling Law for 1-bit Neural Networks. In this paper, we present the first theoretical result that rigorously establishes this scaling law for 1-bit models. We prove that, despite the constraint of weights restricted to $\{-1, +1\}$, the dynamics of model training inevitably align with kernel behavior as the network width grows. This theoretical breakthrough guarantees convergence of the 1-bit model to an arbitrarily small loss as width increases. Furthermore, we introduce the concept of the generalization difference, defined as the gap between the outputs of 1-bit networks and their full-precision counterparts, and demonstrate that this difference maintains a negligible level as network width scales. Building on the work of Kaplan et al. (2020), we conclude by examining how the training loss scales as a power-law function of the model size, dataset size, and computational resources utilized for training. Our findings underscore the promising potential of scaling 1-bit neural networks, suggesting that int1 could become the standard in future neural network precision.
Coupling without Communication and Drafter-Invariant Speculative Decoding
Aug 15, 2024
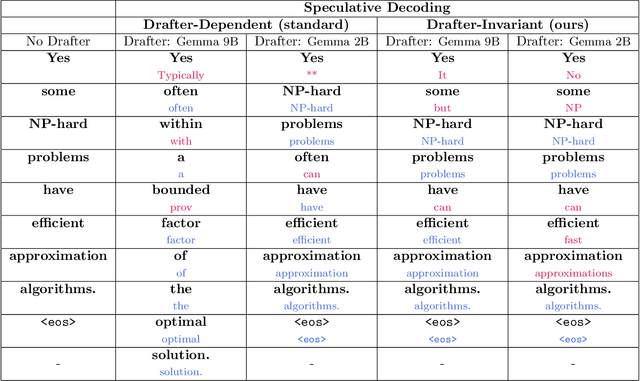
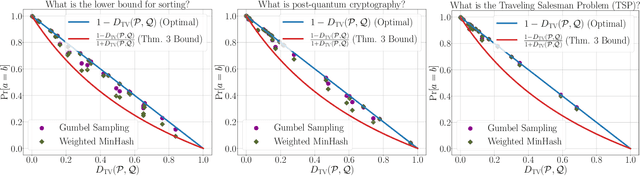

Abstract:Suppose Alice has a distribution $P$ and Bob has a distribution $Q$. Alice wants to generate a sample $a\sim P$ and Bob a sample $b \sim Q$ such that $a = b$ with has as high of probability as possible. It is well-known that, by sampling from an optimal coupling between the distributions, Alice and Bob can achieve $Pr[a = b] = 1 - D_{TV}(P,Q)$, where $D_{TV}(P,Q)$ is the total variation distance. What if Alice and Bob must solve this same problem without communicating at all? Perhaps surprisingly, with access to public randomness, they can still achieve $Pr[a = b] \geq \frac{1 - D_{TV}(P,Q)}{1 + D_{TV}(P,Q)} \geq 1-2D_{TV}(P,Q)$. In fact, this bound can be obtained using a simple protocol based on the Weighted MinHash algorithm. In this work, we explore the communication-free coupling in greater depth. First, we show that an equally simple protocol based on Gumbel sampling matches the worst-case guarantees of the Weighted MinHash approach, but tends to perform better in practice. Conversely, we prove that both approaches are actually sharp: no communication-free protocol can achieve $Pr[a=b]>\frac{1 - D_{TV}(P,Q)}{1 + D_{TV}(P,Q)}$ in the worst-case. Finally, we prove that, for distributions over $n$ items, there exists a scheme that uses just $O(\log(n/\epsilon))$ bits of communication to achieve $Pr[a = b] = 1 - D_{TV}(P,Q) - \epsilon$, i.e. to essentially match optimal coupling. Beyond our theoretical results, we demonstrate an application of communication-free coupling to speculative decoding, a recent method for accelerating autoregressive large language models [Leviathan, Kalman, Matias, ICML 2023]. We show that communication-free protocols yield a variant of speculative decoding that we call Drafter-Invariant Speculative Decoding, which has the desirable property that the output of the method is fixed given a fixed random seed, regardless of what drafter is used for speculation.
QJL: 1-Bit Quantized JL Transform for KV Cache Quantization with Zero Overhead
Jun 05, 2024



Abstract:Serving LLMs requires substantial memory due to the storage requirements of Key-Value (KV) embeddings in the KV cache, which grows with sequence length. An effective approach to compress KV cache is quantization. However, traditional quantization methods face significant memory overhead due to the need to store quantization constants (at least a zero point and a scale) in full precision per data block. Depending on the block size, this overhead can add 1 or 2 bits per quantized number. We introduce QJL, a new quantization approach that consists of a Johnson-Lindenstrauss (JL) transform followed by sign-bit quantization. In contrast to existing methods, QJL eliminates memory overheads by removing the need for storing quantization constants. We propose an asymmetric estimator for the inner product of two vectors and demonstrate that applying QJL to one vector and a standard JL transform without quantization to the other provides an unbiased estimator with minimal distortion. We have developed an efficient implementation of the QJL sketch and its corresponding inner product estimator, incorporating a lightweight CUDA kernel for optimized computation. When applied across various LLMs and NLP tasks to quantize the KV cache to only 3 bits, QJL demonstrates a more than fivefold reduction in KV cache memory usage without compromising accuracy, all while achieving faster runtime. Codes are available at \url{https://github.com/amirzandieh/QJL}.
KDEformer: Accelerating Transformers via Kernel Density Estimation
Feb 05, 2023



Abstract:Dot-product attention mechanism plays a crucial role in modern deep architectures (e.g., Transformer) for sequence modeling, however, na\"ive exact computation of this model incurs quadratic time and memory complexities in sequence length, hindering the training of long-sequence models. Critical bottlenecks are due to the computation of partition functions in the denominator of softmax function as well as the multiplication of the softmax matrix with the matrix of values. Our key observation is that the former can be reduced to a variant of the kernel density estimation (KDE) problem, and an efficient KDE solver can be further utilized to accelerate the latter via subsampling-based fast matrix products. Our proposed KDEformer can approximate the attention in sub-quadratic time with provable spectral norm bounds, while all prior results merely provide entry-wise error bounds. Empirically, we verify that KDEformer outperforms other attention approximations in terms of accuracy, memory, and runtime on various pre-trained models. On BigGAN image generation, we achieve better generative scores than the exact computation with over $4\times$ speedup. For ImageNet classification with T2T-ViT, KDEformer shows over $18\times$ speedup while the accuracy drop is less than $0.5\%$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge