TNT: Improving Chunkwise Training for Test-Time Memorization

Recurrent neural networks (RNNs) with deep test-time memorization modules, such as Titans and TTT, represent a promising, linearly-scaling paradigm distinct from Transformers. While these expressive models do not yet match the peak performance of state-of-the-art Transformers, their potential has been largely untapped due to prohibitively slow training and low hardware utilization. Existing parallelization methods force a fundamental conflict governed by the chunksize hyperparameter: large chunks boost speed but degrade performance, necessitating a fixed, suboptimal compromise. To solve this challenge, we introduce TNT, a novel training paradigm that decouples training efficiency from inference performance through a two-stage process. Stage one is an efficiency-focused pre-training phase utilizing a hierarchical memory. A global module processes large, hardware-friendly chunks for long-range context, while multiple parallel local modules handle fine-grained details. Crucially, by periodically resetting local memory states, we break sequential dependencies to enable massive context parallelization. Stage two is a brief fine-tuning phase where only the local memory modules are adapted to a smaller, high-resolution chunksize, maximizing accuracy with minimal overhead. Evaluated on Titans and TTT models, TNT achieves a substantial acceleration in training speed-up to 17 times faster than the most accurate baseline configuration - while simultaneously improving model accuracy. This improvement removes a critical scalability barrier, establishing a practical foundation for developing expressive RNNs and facilitating future work to close the performance gap with Transformers.

ATLAS: Learning to Optimally Memorize the Context at Test Time

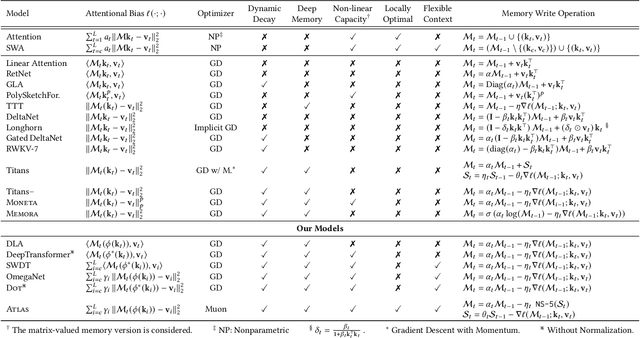
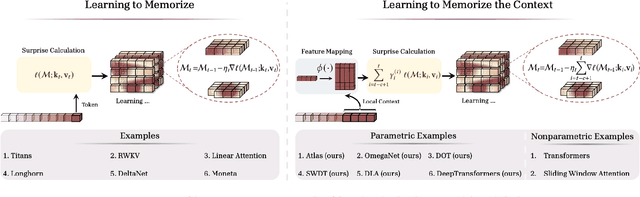
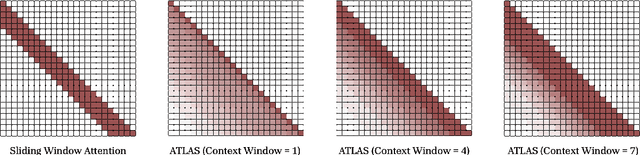
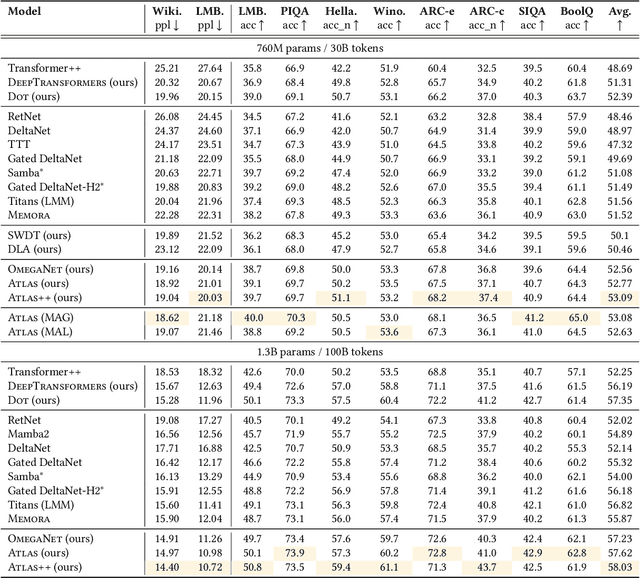
Transformers have been established as the most popular backbones in sequence modeling, mainly due to their effectiveness in in-context retrieval tasks and the ability to learn at scale. Their quadratic memory and time complexity, however, bound their applicability in longer sequences and so has motivated researchers to explore effective alternative architectures such as modern recurrent neural networks (a.k.a long-term recurrent memory module). Despite their recent success in diverse downstream tasks, they struggle in tasks that requires long context understanding and extrapolation to longer sequences. We observe that these shortcomings come from three disjoint aspects in their design: (1) limited memory capacity that is bounded by the architecture of memory and feature mapping of the input; (2) online nature of update, i.e., optimizing the memory only with respect to the last input; and (3) less expressive management of their fixed-size memory. To enhance all these three aspects, we present ATLAS, a long-term memory module with high capacity that learns to memorize the context by optimizing the memory based on the current and past tokens, overcoming the online nature of long-term memory models. Building on this insight, we present a new family of Transformer-like architectures, called DeepTransformers, that are strict generalizations of the original Transformer architecture. Our experimental results on language modeling, common-sense reasoning, recall-intensive, and long-context understanding tasks show that ATLAS surpasses the performance of Transformers and recent linear recurrent models. ATLAS further improves the long context performance of Titans, achieving +80\% accuracy in 10M context length of BABILong benchmark.

Synthetic Text Generation for Training Large Language Models via Gradient Matching

Synthetic data has the potential to improve the performance, training efficiency, and privacy of real training examples. Nevertheless, existing approaches for synthetic text generation are mostly heuristics and cannot generate human-readable text without compromising the privacy of real data or provide performance guarantees for training Large Language Models (LLMs). In this work, we propose the first theoretically rigorous approach for generating synthetic human-readable text that guarantees the convergence and performance of LLMs during fine-tuning on a target task. To do so, we leverage Alternating Direction Method of Multipliers (ADMM) that iteratively optimizes the embeddings of synthetic examples to match the gradient of the target training or validation data, and maps them to a sequence of text tokens with low perplexity. In doing so, the generated synthetic text can guarantee convergence of the model to a close neighborhood of the solution obtained by fine-tuning on real data. Experiments on various classification tasks confirm the effectiveness of our proposed approach.

PiKE: Adaptive Data Mixing for Multi-Task Learning Under Low Gradient Conflicts

Modern machine learning models are trained on diverse datasets and tasks to improve generalization. A key challenge in multitask learning is determining the optimal data mixing and sampling strategy across different data sources. Prior research in this multi-task learning setting has primarily focused on mitigating gradient conflicts between tasks. However, we observe that many real-world multitask learning scenarios-such as multilingual training and multi-domain learning in large foundation models-exhibit predominantly positive task interactions with minimal or no gradient conflict. Building on this insight, we introduce PiKE (Positive gradient interaction-based K-task weights Estimator), an adaptive data mixing algorithm that dynamically adjusts task contributions throughout training. PiKE optimizes task sampling to minimize overall loss, effectively leveraging positive gradient interactions with almost no additional computational overhead. We establish theoretical convergence guarantees for PiKE and demonstrate its superiority over static and non-adaptive mixing strategies. Additionally, we extend PiKE to promote fair learning across tasks, ensuring balanced progress and preventing task underrepresentation. Empirical evaluations on large-scale language model pretraining show that PiKE consistently outperforms existing heuristic and static mixing strategies, leading to faster convergence and improved downstream task performance.

Addax: Utilizing Zeroth-Order Gradients to Improve Memory Efficiency and Performance of SGD for Fine-Tuning Language Models

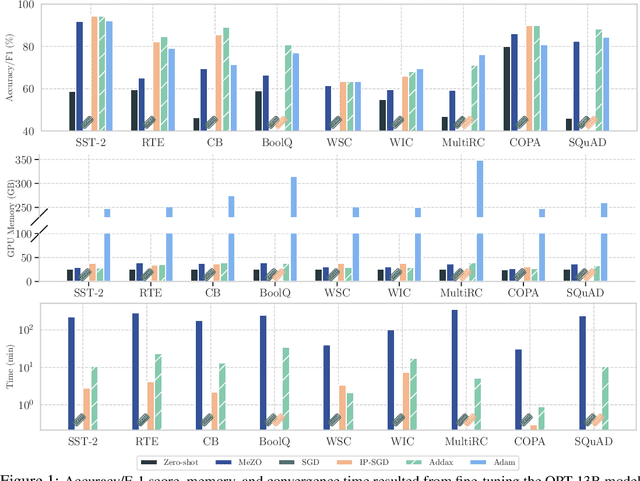
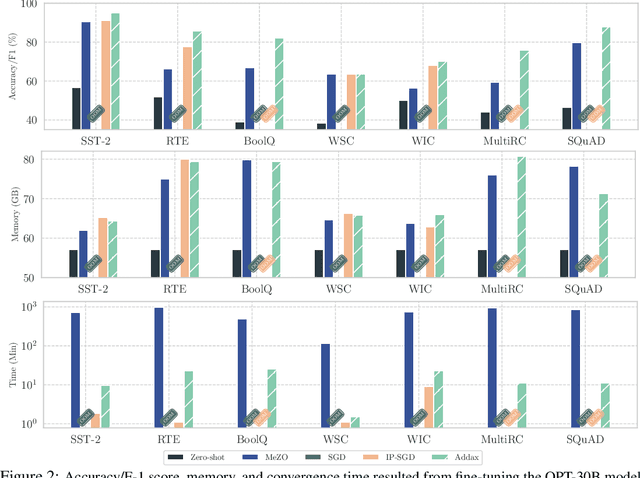
Fine-tuning language models (LMs) with the Adam optimizer often demands excessive memory, limiting accessibility. The "in-place" version of Stochastic Gradient Descent (IP-SGD) and Memory-Efficient Zeroth-order Optimizer (MeZO) have been proposed to address this. However, IP-SGD still requires substantial memory, and MeZO suffers from slow convergence and degraded final performance due to its zeroth-order nature. This paper introduces Addax, a novel method that improves both memory efficiency and performance of IP-SGD by integrating it with MeZO. Specifically, Addax computes zeroth- or first-order gradients of data points in the minibatch based on their memory consumption, combining these gradient estimates to update directions. By computing zeroth-order gradients for data points that require more memory and first-order gradients for others, Addax overcomes the slow convergence of MeZO and the excessive memory requirement of IP-SGD. Additionally, the zeroth-order gradient acts as a regularizer for the first-order gradient, further enhancing the model's final performance. Theoretically, we establish the convergence of Addax under mild assumptions, demonstrating faster convergence and less restrictive hyper-parameter choices than MeZO. Our experiments with diverse LMs and tasks show that Addax consistently outperforms MeZO regarding accuracy and convergence speed while having a comparable memory footprint. When fine-tuning OPT-13B with one A100 GPU, on average, Addax outperforms MeZO in accuracy/F1 score by 14% and runs 15x faster while using memory similar to MeZO. In our experiments on the larger OPT-30B model, on average, Addax outperforms MeZO in terms of accuracy/F1 score by >16 and runs 30x faster on a single H100 GPU. Moreover, Addax surpasses the performance of standard fine-tuning approaches, such as IP-SGD and Adam, in most tasks with significantly less memory requirement.

Optimal Differentially Private Learning with Public Data

Differential Privacy (DP) ensures that training a machine learning model does not leak private data. However, the cost of DP is lower model accuracy or higher sample complexity. In practice, we may have access to auxiliary public data that is free of privacy concerns. This has motivated the recent study of what role public data might play in improving the accuracy of DP models. In this work, we assume access to a given amount of public data and settle the following fundamental open questions: 1. What is the optimal (worst-case) error of a DP model trained over a private data set while having access to side public data? What algorithms are optimal? 2. How can we harness public data to improve DP model training in practice? We consider these questions in both the local and central models of DP. To answer the first question, we prove tight (up to constant factors) lower and upper bounds that characterize the optimal error rates of three fundamental problems: mean estimation, empirical risk minimization, and stochastic convex optimization. We prove that public data reduces the sample complexity of DP model training. Perhaps surprisingly, we show that the optimal error rates can be attained (up to constants) by either discarding private data and training a public model, or treating public data like it's private data and using an optimal DP algorithm. To address the second question, we develop novel algorithms which are "even more optimal" (i.e. better constants) than the asymptotically optimal approaches described above. For local DP mean estimation with public data, our algorithm is optimal including constants. Empirically, our algorithms show benefits over existing approaches for DP model training with side access to public data.