Optimal Differentially Private Learning with Public Data

Differential Privacy (DP) ensures that training a machine learning model does not leak private data. However, the cost of DP is lower model accuracy or higher sample complexity. In practice, we may have access to auxiliary public data that is free of privacy concerns. This has motivated the recent study of what role public data might play in improving the accuracy of DP models. In this work, we assume access to a given amount of public data and settle the following fundamental open questions: 1. What is the optimal (worst-case) error of a DP model trained over a private data set while having access to side public data? What algorithms are optimal? 2. How can we harness public data to improve DP model training in practice? We consider these questions in both the local and central models of DP. To answer the first question, we prove tight (up to constant factors) lower and upper bounds that characterize the optimal error rates of three fundamental problems: mean estimation, empirical risk minimization, and stochastic convex optimization. We prove that public data reduces the sample complexity of DP model training. Perhaps surprisingly, we show that the optimal error rates can be attained (up to constants) by either discarding private data and training a public model, or treating public data like it's private data and using an optimal DP algorithm. To address the second question, we develop novel algorithms which are "even more optimal" (i.e. better constants) than the asymptotically optimal approaches described above. For local DP mean estimation with public data, our algorithm is optimal including constants. Empirically, our algorithms show benefits over existing approaches for DP model training with side access to public data.

A Rigorous Study of Integrated Gradients Method and Extensions to Internal Neuron Attributions

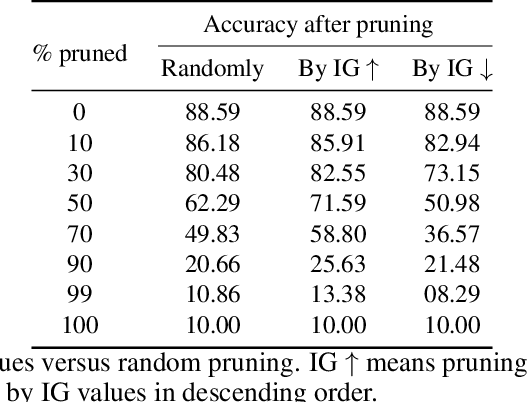
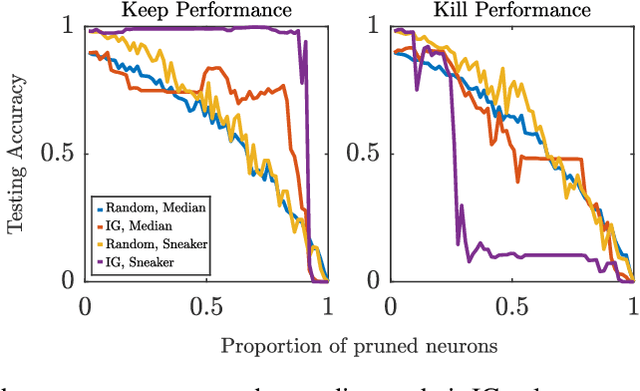
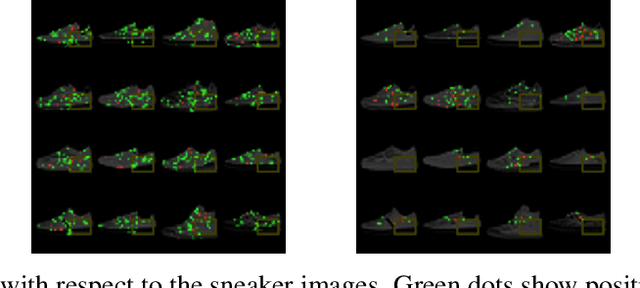
As the efficacy of deep learning (DL) grows, so do concerns about the lack of transparency of these black-box models. Attribution methods aim to improve transparency of DL models by quantifying an input feature's importance to a model's prediction. The method of Integrated gradients (IG) sets itself apart by claiming other methods failed to satisfy desirable axioms, while IG and methods like it uniquely satisfied said axioms. This paper comments on fundamental aspects of IG and its applications/extensions: 1) We identify key unaddressed differences between DL-attribution function spaces and the supporting literature's function spaces which problematize previous claims of IG uniqueness. We show that with the introduction of an additional axiom, $\textit{non-decreasing positivity}$, the uniqueness claim can be established. 2) We address the question of input sensitivity by identifying function spaces where the IG is/is not Lipschitz continuous in the attributed input. 3) We show how axioms for single-baseline methods in IG impart analogous properties for methods where the baseline is a probability distribution over the input sample space. 4) We introduce a means of decomposing the IG map with respect to a layer of internal neurons while simultaneously gaining internal-neuron attributions. Finally, we present experimental results validating the decomposition and internal neuron attributions.

DAIR: Data Augmented Invariant Regularization

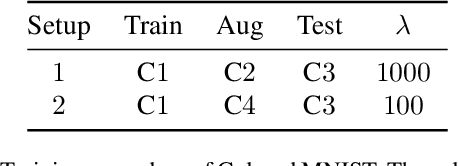
While deep learning through empirical risk minimization (ERM) has succeeded at achieving human-level performance at a variety of complex tasks, ERM generalizes poorly to distribution shift. This is partly explained by overfitting to spurious features such as background in images or named entities in natural language. Synthetic data augmentation followed by empirical risk minimization (DA-ERM) is a simple yet powerful solution to remedy this problem. In this paper, we propose data augmented invariant regularization (DAIR). The idea of DAIR is based on the observation that the model performance (loss) is desired to be consistent on the augmented sample and the original one. DAIR introduces a regularizer on DA-ERM to penalize such loss inconsistency. Both theoretically and through empirical experiments, we show that a particular form of the DAIR regularizer consistently performs well in a variety of settings. We apply it to multiple real-world learning problems involving domain shift, namely robust regression, visual question answering, robust deep neural network training, and task-oriented dialog modeling. Our experiments show that DAIR consistently outperforms ERM and DA-ERM with little marginal cost and setting new state-of-the-art results in several benchmarks.

A Decentralized Adaptive Momentum Method for Solving a Class of Min-Max Optimization Problems

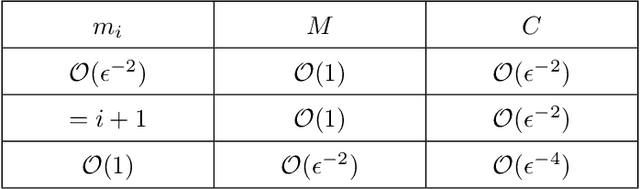
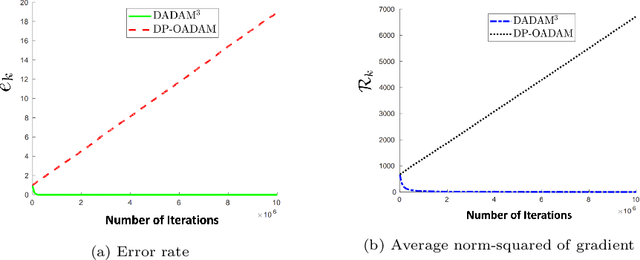
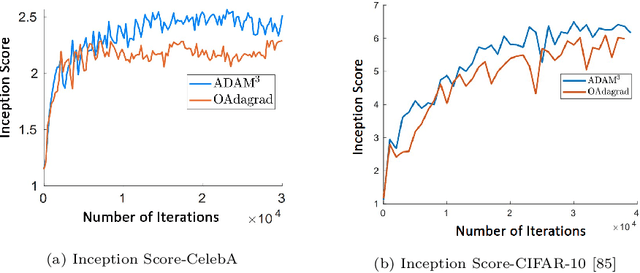
Min-max saddle point games have recently been intensely studied, due to their wide range of applications, including training Generative Adversarial Networks (GANs). However, most of the recent efforts for solving them are limited to special regimes such as convex-concave games. Further, it is customarily assumed that the underlying optimization problem is solved either by a single machine or in the case of multiple machines connected in centralized fashion, wherein each one communicates with a central node. The latter approach becomes challenging, when the underlying communications network has low bandwidth. In addition, privacy considerations may dictate that certain nodes can communicate with a subset of other nodes. Hence, it is of interest to develop methods that solve min-max games in a decentralized manner. To that end, we develop a decentralized adaptive momentum (ADAM)-type algorithm for solving min-max optimization problem under the condition that the objective function satisfies a Minty Variational Inequality condition, which is a generalization to convex-concave case. The proposed method overcomes shortcomings of recent non-adaptive gradient-based decentralized algorithms for min-max optimization problems that do not perform well in practice and require careful tuning. In this paper, we obtain non-asymptotic rates of convergence of the proposed algorithm (coined DADAM$^3$) for finding a (stochastic) first-order Nash equilibrium point and subsequently evaluate its performance on training GANs. The extensive empirical evaluation shows that DADAM$^3$ outperforms recently developed methods, including decentralized optimistic stochastic gradient for solving such min-max problems.

Alternating Direction Method of Multipliers for Quantization

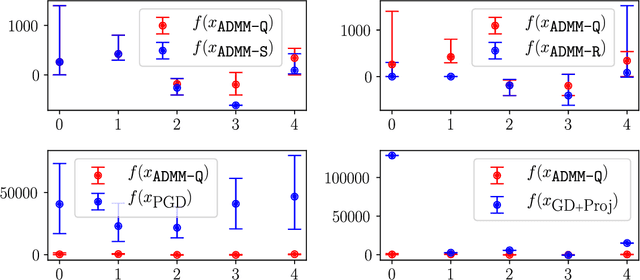
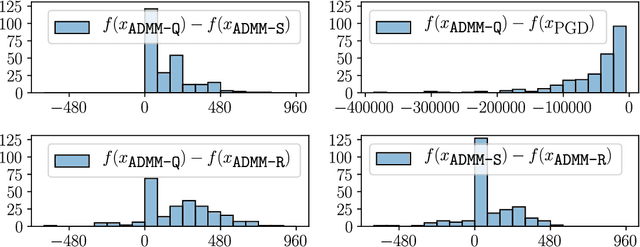
Quantization of the parameters of machine learning models, such as deep neural networks, requires solving constrained optimization problems, where the constraint set is formed by the Cartesian product of many simple discrete sets. For such optimization problems, we study the performance of the Alternating Direction Method of Multipliers for Quantization ($\texttt{ADMM-Q}$) algorithm, which is a variant of the widely-used ADMM method applied to our discrete optimization problem. We establish the convergence of the iterates of $\texttt{ADMM-Q}$ to certain $\textit{stationary points}$. To the best of our knowledge, this is the first analysis of an ADMM-type method for problems with discrete variables/constraints. Based on our theoretical insights, we develop a few variants of $\texttt{ADMM-Q}$ that can handle inexact update rules, and have improved performance via the use of "soft projection" and "injecting randomness to the algorithm". We empirically evaluate the efficacy of our proposed approaches.