Four Axiomatic Characterizations of the Integrated Gradients Attribution Method

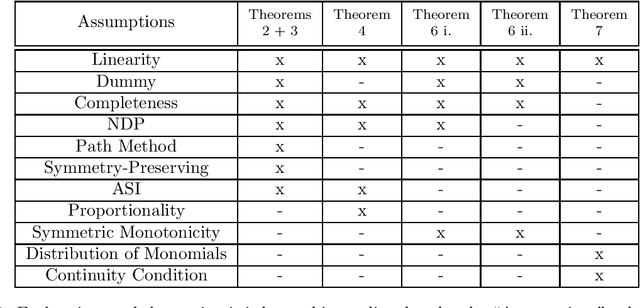
Deep neural networks have produced significant progress among machine learning models in terms of accuracy and functionality, but their inner workings are still largely unknown. Attribution methods seek to shine a light on these "black box" models by indicating how much each input contributed to a model's outputs. The Integrated Gradients (IG) method is a state of the art baseline attribution method in the axiomatic vein, meaning it is designed to conform to particular principles of attributions. We present four axiomatic characterizations of IG, establishing IG as the unique method to satisfy different sets of axioms among a class of attribution methods.

Distributing Synergy Functions: Unifying Game-Theoretic Interaction Methods for Machine-Learning Explainability

Deep learning has revolutionized many areas of machine learning, from computer vision to natural language processing, but these high-performance models are generally "black box." Explaining such models would improve transparency and trust in AI-powered decision making and is necessary for understanding other practical needs such as robustness and fairness. A popular means of enhancing model transparency is to quantify how individual inputs contribute to model outputs (called attributions) and the magnitude of interactions between groups of inputs. A growing number of these methods import concepts and results from game theory to produce attributions and interactions. This work presents a unifying framework for game-theory-inspired attribution and $k^\text{th}$-order interaction methods. We show that, given modest assumptions, a unique full account of interactions between features, called synergies, is possible in the continuous input setting. We identify how various methods are characterized by their policy of distributing synergies. We also demonstrate that gradient-based methods are characterized by their actions on monomials, a type of synergy function, and introduce unique gradient-based methods. We show that the combination of various criteria uniquely defines the attribution/interaction methods. Thus, the community needs to identify goals and contexts when developing and employing attribution and interaction methods.

A Rigorous Study of Integrated Gradients Method and Extensions to Internal Neuron Attributions

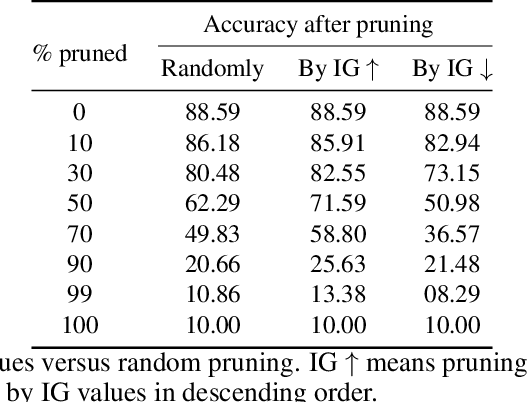
As the efficacy of deep learning (DL) grows, so do concerns about the lack of transparency of these black-box models. Attribution methods aim to improve transparency of DL models by quantifying an input feature's importance to a model's prediction. The method of Integrated gradients (IG) sets itself apart by claiming other methods failed to satisfy desirable axioms, while IG and methods like it uniquely satisfied said axioms. This paper comments on fundamental aspects of IG and its applications/extensions: 1) We identify key unaddressed differences between DL-attribution function spaces and the supporting literature's function spaces which problematize previous claims of IG uniqueness. We show that with the introduction of an additional axiom, $\textit{non-decreasing positivity}$, the uniqueness claim can be established. 2) We address the question of input sensitivity by identifying function spaces where the IG is/is not Lipschitz continuous in the attributed input. 3) We show how axioms for single-baseline methods in IG impart analogous properties for methods where the baseline is a probability distribution over the input sample space. 4) We introduce a means of decomposing the IG map with respect to a layer of internal neurons while simultaneously gaining internal-neuron attributions. Finally, we present experimental results validating the decomposition and internal neuron attributions.

Explainability Tools Enabling Deep Learning in Future In-Situ Real-Time Planetary Explorations

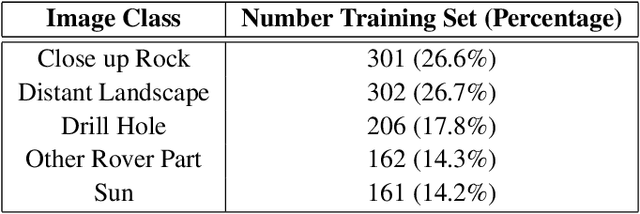
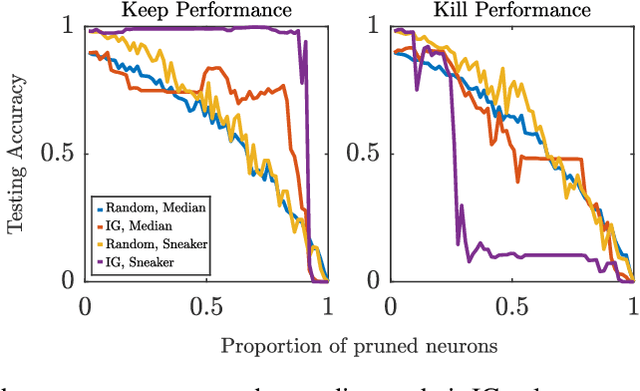
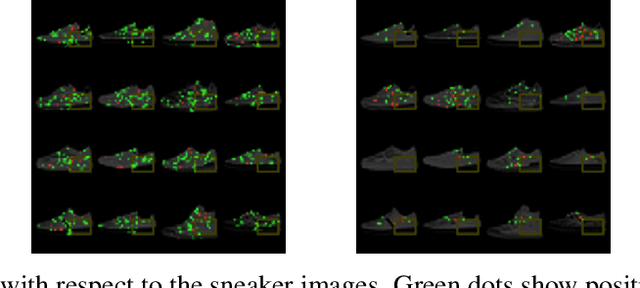
Deep learning (DL) has proven to be an effective machine learning and computer vision technique. DL-based image segmentation, object recognition and classification will aid many in-situ Mars rover tasks such as path planning and artifact recognition/extraction. However, most of the Deep Neural Network (DNN) architectures are so complex that they are considered a 'black box'. In this paper, we used integrated gradients to describe the attributions of each neuron to the output classes. It provides a set of explainability tools (ET) that opens the black box of a DNN so that the individual contribution of neurons to category classification can be ranked and visualized. The neurons in each dense layer are mapped and ranked by measuring expected contribution of a neuron to a class vote given a true image label. The importance of neurons is prioritized according to their correct or incorrect contribution to the output classes and suppression or bolstering of incorrect classes, weighted by the size of each class. ET provides an interface to prune the network to enhance high-rank neurons and remove low-performing neurons. ET technology will make DNNs smaller and more efficient for implementation in small embedded systems. It also leads to more explainable and testable DNNs that can make systems easier for Validation \& Verification. The goal of ET technology is to enable the adoption of DL in future in-situ planetary exploration missions.