A Rigorous Study of Integrated Gradients Method and Extensions to Internal Neuron Attributions

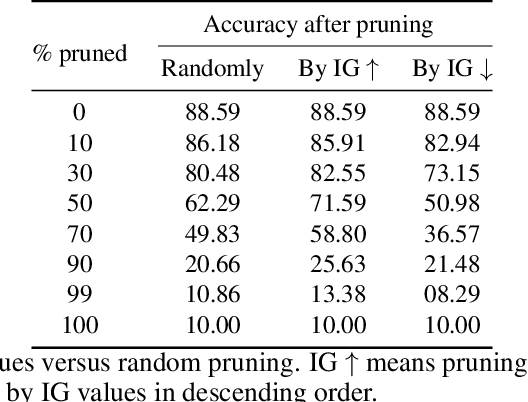
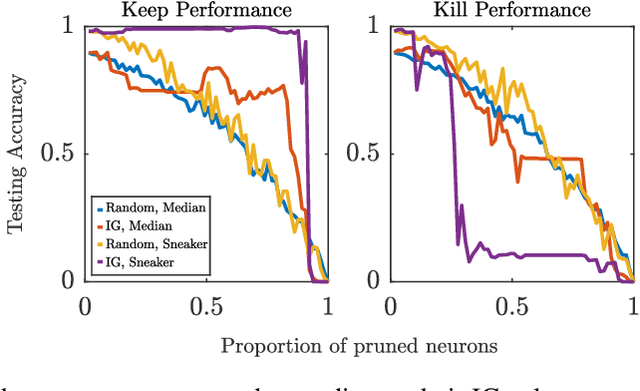
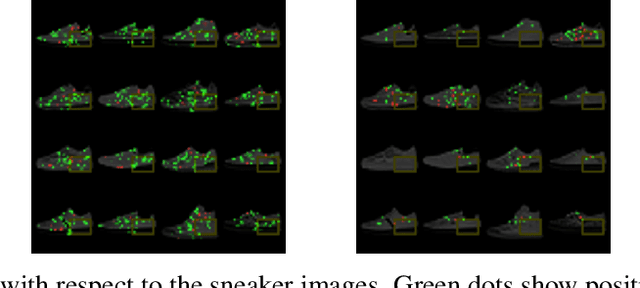
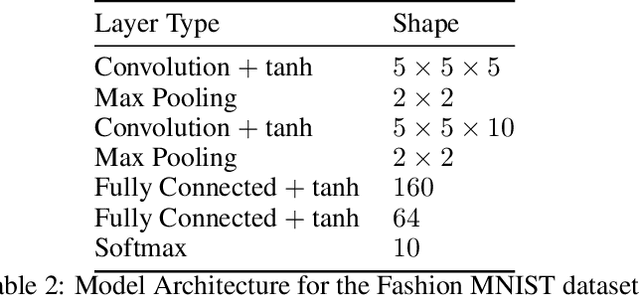
As the efficacy of deep learning (DL) grows, so do concerns about the lack of transparency of these black-box models. Attribution methods aim to improve transparency of DL models by quantifying an input feature's importance to a model's prediction. The method of Integrated gradients (IG) sets itself apart by claiming other methods failed to satisfy desirable axioms, while IG and methods like it uniquely satisfied said axioms. This paper comments on fundamental aspects of IG and its applications/extensions: 1) We identify key unaddressed differences between DL-attribution function spaces and the supporting literature's function spaces which problematize previous claims of IG uniqueness. We show that with the introduction of an additional axiom, $\textit{non-decreasing positivity}$, the uniqueness claim can be established. 2) We address the question of input sensitivity by identifying function spaces where the IG is/is not Lipschitz continuous in the attributed input. 3) We show how axioms for single-baseline methods in IG impart analogous properties for methods where the baseline is a probability distribution over the input sample space. 4) We introduce a means of decomposing the IG map with respect to a layer of internal neurons while simultaneously gaining internal-neuron attributions. Finally, we present experimental results validating the decomposition and internal neuron attributions.