Nonconvex-Nonconcave Min-Max Optimization with a Small Maximization Domain

We study the problem of finding approximate first-order stationary points in optimization problems of the form $\min_{x \in X} \max_{y \in Y} f(x,y)$, where the sets $X,Y$ are convex and $Y$ is compact. The objective function $f$ is smooth, but assumed neither convex in $x$ nor concave in $y$. Our approach relies upon replacing the function $f(x,\cdot)$ with its $k$th order Taylor approximation (in $y$) and finding a near-stationary point in the resulting surrogate problem. To guarantee its success, we establish the following result: let the Euclidean diameter of $Y$ be small in terms of the target accuracy $\varepsilon$, namely $O(\varepsilon^{\frac{2}{k+1}})$ for $k \in \mathbb{N}$ and $O(\varepsilon)$ for $k = 0$, with the constant factors controlled by certain regularity parameters of $f$; then any $\varepsilon$-stationary point in the surrogate problem remains $O(\varepsilon)$-stationary for the initial problem. Moreover, we show that these upper bounds are nearly optimal: the aforementioned reduction provably fails when the diameter of $Y$ is larger. For $0 \le k \le 2$ the surrogate function can be efficiently maximized in $y$; our general approximation result then leads to efficient algorithms for finding a near-stationary point in nonconvex-nonconcave min-max problems, for which we also provide convergence guarantees.

A Decentralized Adaptive Momentum Method for Solving a Class of Min-Max Optimization Problems

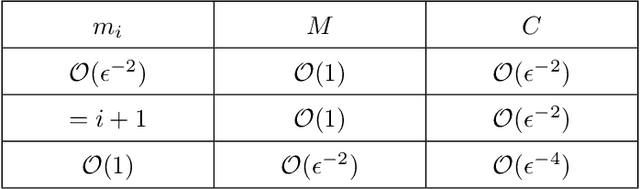
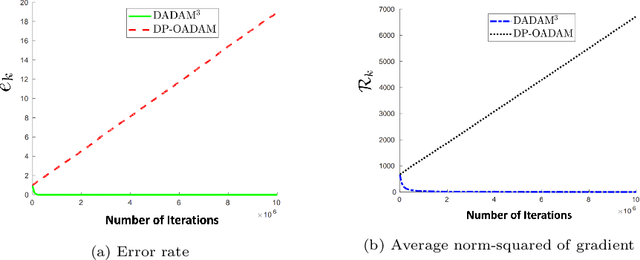
Min-max saddle point games have recently been intensely studied, due to their wide range of applications, including training Generative Adversarial Networks (GANs). However, most of the recent efforts for solving them are limited to special regimes such as convex-concave games. Further, it is customarily assumed that the underlying optimization problem is solved either by a single machine or in the case of multiple machines connected in centralized fashion, wherein each one communicates with a central node. The latter approach becomes challenging, when the underlying communications network has low bandwidth. In addition, privacy considerations may dictate that certain nodes can communicate with a subset of other nodes. Hence, it is of interest to develop methods that solve min-max games in a decentralized manner. To that end, we develop a decentralized adaptive momentum (ADAM)-type algorithm for solving min-max optimization problem under the condition that the objective function satisfies a Minty Variational Inequality condition, which is a generalization to convex-concave case. The proposed method overcomes shortcomings of recent non-adaptive gradient-based decentralized algorithms for min-max optimization problems that do not perform well in practice and require careful tuning. In this paper, we obtain non-asymptotic rates of convergence of the proposed algorithm (coined DADAM$^3$) for finding a (stochastic) first-order Nash equilibrium point and subsequently evaluate its performance on training GANs. The extensive empirical evaluation shows that DADAM$^3$ outperforms recently developed methods, including decentralized optimistic stochastic gradient for solving such min-max problems.

Efficient Algorithms for Estimating the Parameters of Mixed Linear Regression Models

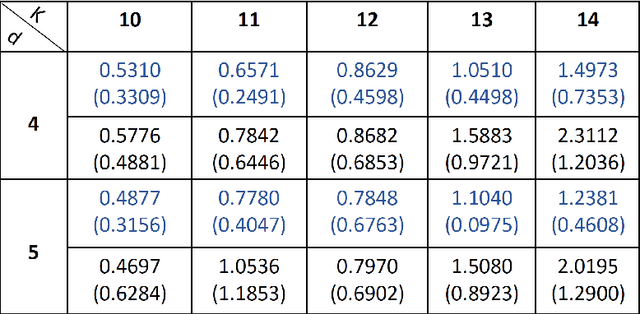
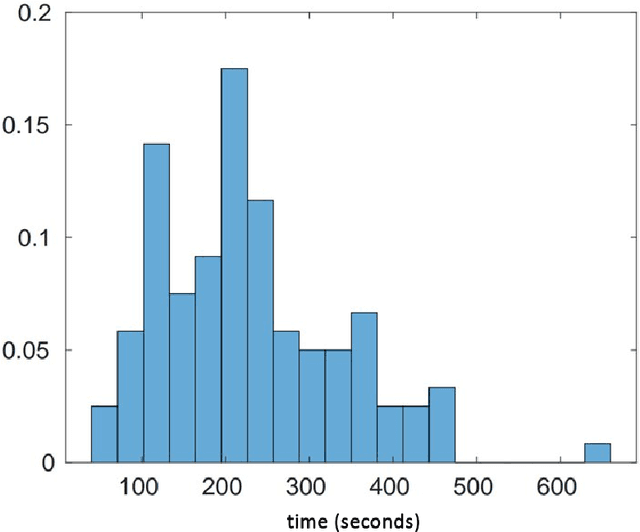
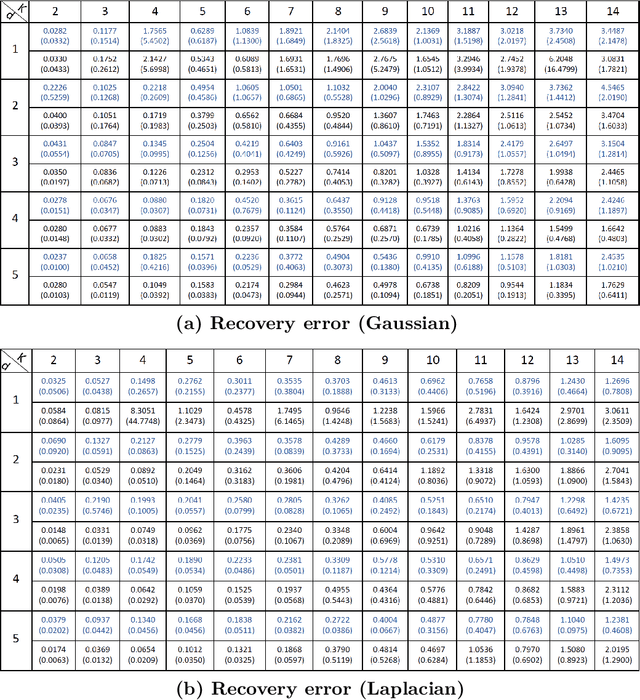
Mixed linear regression (MLR) model is among the most exemplary statistical tools for modeling non-linear distributions using a mixture of linear models. When the additive noise in MLR model is Gaussian, Expectation-Maximization (EM) algorithm is a widely-used algorithm for maximum likelihood estimation of MLR parameters. However, when noise is non-Gaussian, the steps of EM algorithm may not have closed-form update rules, which makes EM algorithm impractical. In this work, we study the maximum likelihood estimation of the parameters of MLR model when the additive noise has non-Gaussian distribution. In particular, we consider the case that noise has Laplacian distribution and we first show that unlike the the Gaussian case, the resulting sub-problems of EM algorithm in this case does not have closed-form update rule, thus preventing us from using EM in this case. To overcome this issue, we propose a new algorithm based on combining the alternating direction method of multipliers (ADMM) with EM algorithm idea. Our numerical experiments show that our method outperforms the EM algorithm in statistical accuracy and computational time in non-Gaussian noise case.

Solving a class of non-convex min-max games using adaptive momentum methods

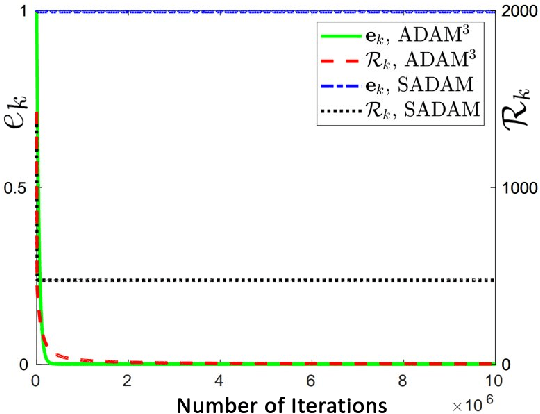
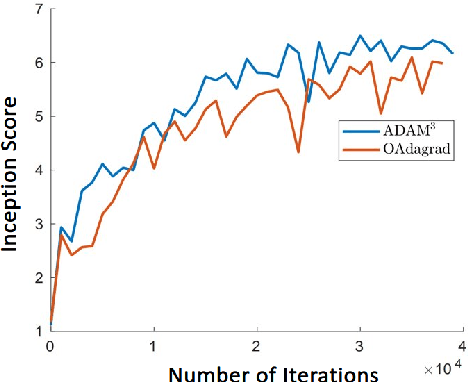
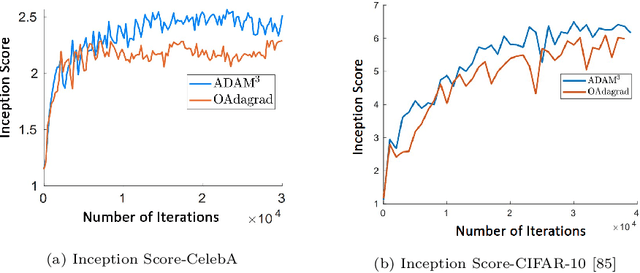
Adaptive momentum methods have recently attracted a lot of attention for training of deep neural networks. They use an exponential moving average of past gradients of the objective function to update both search directions and learning rates. However, these methods are not suited for solving min-max optimization problems that arise in training generative adversarial networks. In this paper, we propose an adaptive momentum min-max algorithm that generalizes adaptive momentum methods to the non-convex min-max regime. Further, we establish non-asymptotic rates of convergence for the proposed algorithm when used in a reasonably broad class of non-convex min-max optimization problems. Experimental results illustrate its superior performance vis-a-vis benchmark methods for solving such problems.

Solving Non-Convex Non-Differentiable Min-Max Games using Proximal Gradient Method

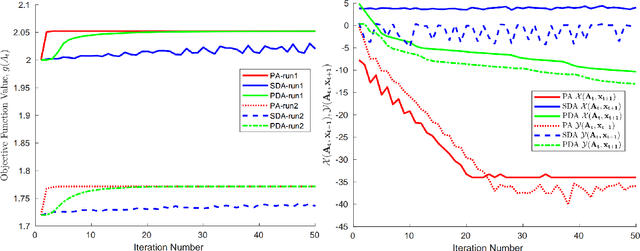
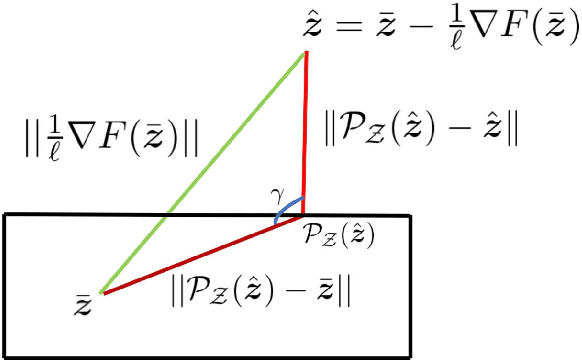
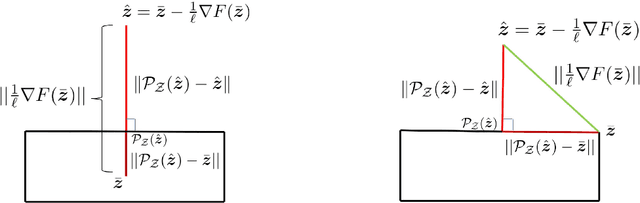
Min-max saddle point games appear in a wide range of applications in machine leaning and signal processing. Despite their wide applicability, theoretical studies are mostly limited to the special convex-concave structure. While some recent works generalized these results to special smooth non-convex cases, our understanding of non-smooth scenarios is still limited. In this work, we study special form of non-smooth min-max games when the objective function is (strongly) convex with respect to one of the player's decision variable. We show that a simple multi-step proximal gradient descent-ascent algorithm converges to $\epsilon$-first-order Nash equilibrium of the min-max game with the number of gradient evaluations being polynomial in $1/\epsilon$. We will also show that our notion of stationarity is stronger than existing ones in the literature. Finally, we evaluate the performance of the proposed algorithm through adversarial attack on a LASSO estimator.

Training generative networks using random discriminators

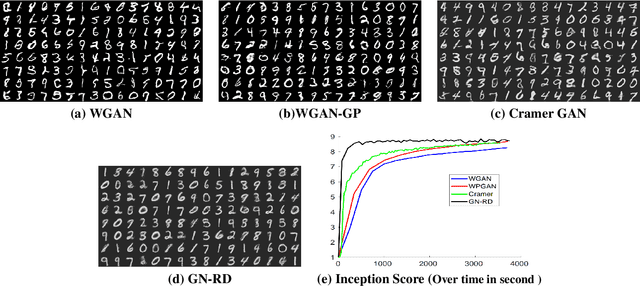
In recent years, Generative Adversarial Networks (GANs) have drawn a lot of attentions for learning the underlying distribution of data in various applications. Despite their wide applicability, training GANs is notoriously difficult. This difficulty is due to the min-max nature of the resulting optimization problem and the lack of proper tools of solving general (non-convex, non-concave) min-max optimization problems. In this paper, we try to alleviate this problem by proposing a new generative network that relies on the use of random discriminators instead of adversarial design. This design helps us to avoid the min-max formulation and leads to an optimization problem that is stable and could be solved efficiently. The performance of the proposed method is evaluated using handwritten digits (MNIST) and Fashion products (Fashion-MNIST) data sets. While the resulting images are not as sharp as adversarial training, the use of random discriminator leads to a much faster algorithm as compared to the adversarial counterpart. This observation, at the minimum, illustrates the potential of the random discriminator approach for warm-start in training GANs.

A Method for Robust Online Classification using Dictionary Learning: Development and Assessment for Monitoring Manual Material Handling Activities Using Wearable Sensors

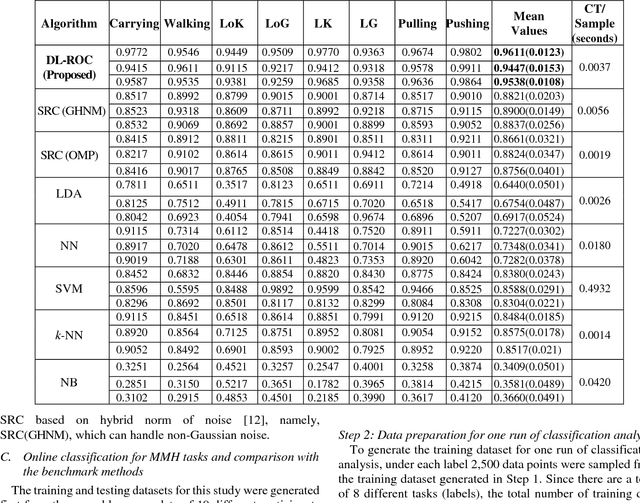
Classification methods based on sparse estimation have drawn much attention recently, due to their effectiveness in processing high-dimensional data such as images. In this paper, a method to improve the performance of a sparse representation classification (SRC) approach is proposed; it is then applied to the problem of online process monitoring of human workers, specifically manual material handling (MMH) operations monitored using wearable sensors (involving 111 sensor channels). Our proposed method optimizes the design matrix (aka dictionary) in the linear model used for SRC, minimizing its ill-posedness to achieve a sparse solution. This procedure is based on the idea of dictionary learning (DL): we optimize the design matrix formed by training datasets to minimize both redundancy and coherency as well as reducing the size of these datasets. Use of such optimized training data can subsequently improve classification accuracy and help decrease the computational time needed for the SRC; it is thus more applicable for online process monitoring. Performance of the proposed methodology is demonstrated using wearable sensor data obtained from manual material handling experiments, and is found to be superior to those of benchmark methods in terms of accuracy, while also requiring computational time appropriate for MMH online monitoring.

On the Behavior of the Expectation-Maximization Algorithm for Mixture Models

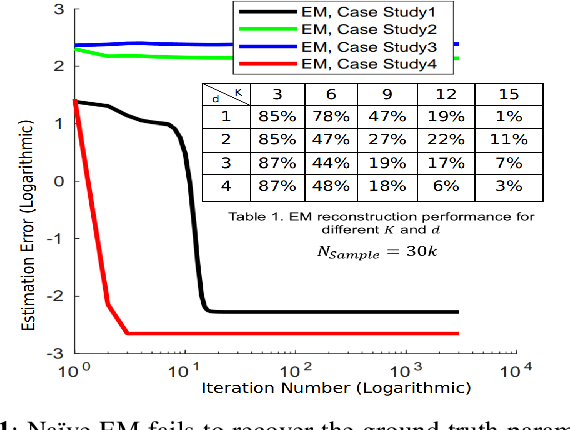
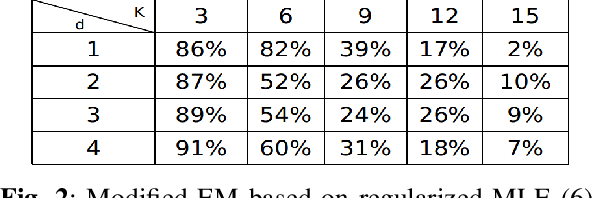
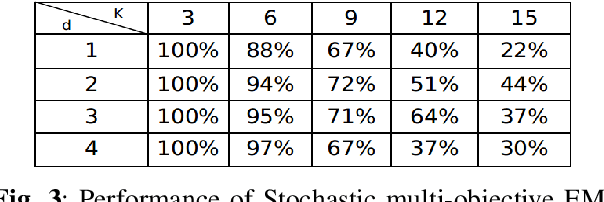
Finite mixture models are among the most popular statistical models used in different data science disciplines. Despite their broad applicability, inference under these models typically leads to computationally challenging non-convex problems. While the Expectation-Maximization (EM) algorithm is the most popular approach for solving these non-convex problems, the behavior of this algorithm is not well understood. In this work, we focus on the case of mixture of Laplacian (or Gaussian) distribution. We start by analyzing a simple equally weighted mixture of two single dimensional Laplacian distributions and show that every local optimum of the population maximum likelihood estimation problem is globally optimal. Then, we prove that the EM algorithm converges to the ground truth parameters almost surely with random initialization. Our result extends the existing results for Gaussian distribution to Laplacian distribution. Then we numerically study the behavior of mixture models with more than two components. Motivated by our extensive numerical experiments, we propose a novel stochastic method for estimating the mean of components of a mixture model. Our numerical experiments show that our algorithm outperforms the Naive EM algorithm in almost all scenarios.