Private Non-Convex Federated Learning Without a Trusted Server

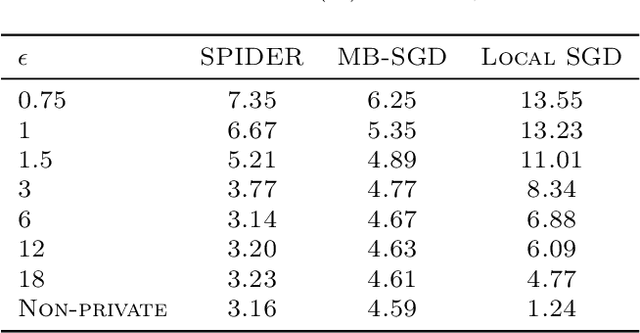
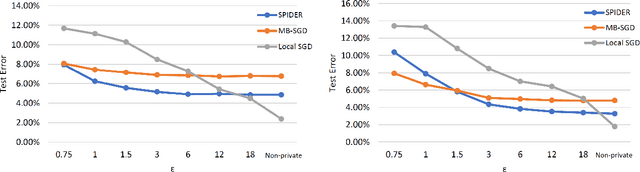
We study differentially private (DP) federated learning (FL) with non-convex loss functions and heterogeneous (non-i.i.d.) client data in the absence of a trusted server, both with and without a secure "shuffler" to anonymize client reports. We propose novel algorithms that satisfy local differential privacy (LDP) at the client level and shuffle differential privacy (SDP) for three classes of Lipschitz continuous loss functions: First, we consider losses satisfying the Proximal Polyak-Lojasiewicz (PL) inequality, which is an extension of the classical PL condition to the constrained setting. Prior works studying DP PL optimization only consider the unconstrained problem with Lipschitz loss functions, which rules out many interesting practical losses, such as strongly convex, least squares, and regularized logistic regression. However, by analyzing the proximal PL scenario, we permit such losses which are Lipschitz on a restricted parameter domain. We propose LDP and SDP algorithms that nearly attain the optimal strongly convex, homogeneous (i.i.d.) rates. Second, we provide the first DP algorithms for non-convex/non-smooth loss functions. Third, we specialize our analysis to smooth, unconstrained non-convex FL. Our bounds improve on the state-of-the-art, even in the special case of a single client, and match the non-private lower bound in certain practical parameter regimes. Numerical experiments show that our algorithm yields better accuracy than baselines for most privacy levels.

Efficient Algorithms for Estimating the Parameters of Mixed Linear Regression Models

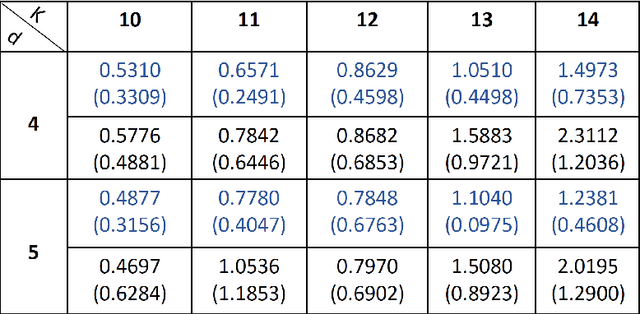
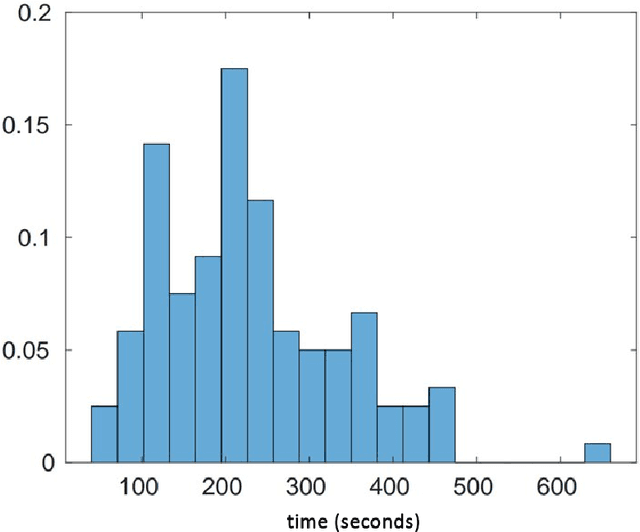
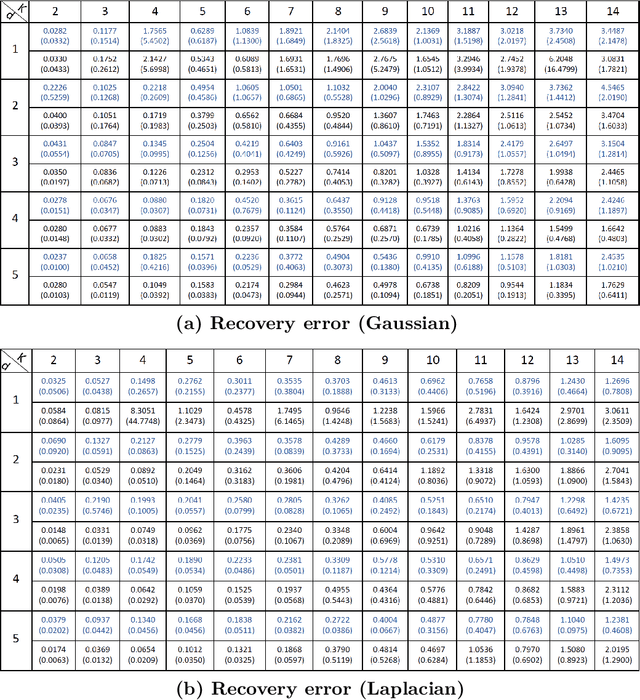
Mixed linear regression (MLR) model is among the most exemplary statistical tools for modeling non-linear distributions using a mixture of linear models. When the additive noise in MLR model is Gaussian, Expectation-Maximization (EM) algorithm is a widely-used algorithm for maximum likelihood estimation of MLR parameters. However, when noise is non-Gaussian, the steps of EM algorithm may not have closed-form update rules, which makes EM algorithm impractical. In this work, we study the maximum likelihood estimation of the parameters of MLR model when the additive noise has non-Gaussian distribution. In particular, we consider the case that noise has Laplacian distribution and we first show that unlike the the Gaussian case, the resulting sub-problems of EM algorithm in this case does not have closed-form update rule, thus preventing us from using EM in this case. To overcome this issue, we propose a new algorithm based on combining the alternating direction method of multipliers (ADMM) with EM algorithm idea. Our numerical experiments show that our method outperforms the EM algorithm in statistical accuracy and computational time in non-Gaussian noise case.