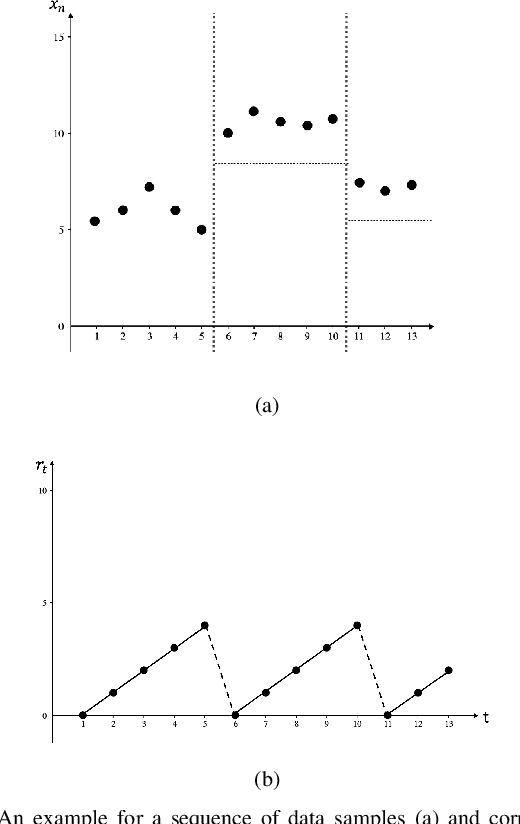
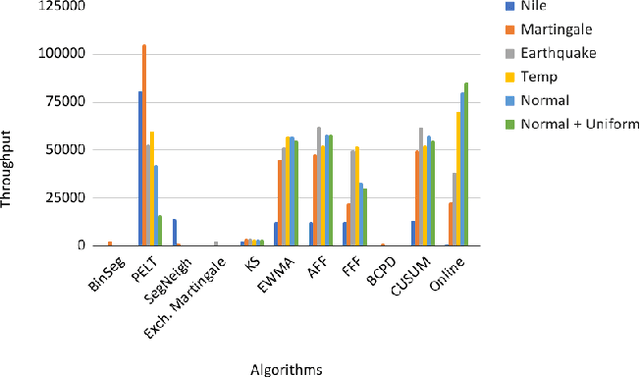
Online Changepoint Detection on a Budget

Changepoints are abrupt variations in the underlying distribution of data. Detecting changes in a data stream is an important problem with many applications. In this paper, we are interested in changepoint detection algorithms which operate in an online setting in the sense that both its storage requirements and worst-case computational complexity per observation are independent of the number of previous observations. We propose an online changepoint detection algorithm for both univariate and multivariate data which compares favorably with offline changepoint detection algorithms while also operating in a strictly more constrained computational model. In addition, we present a simple online hyperparameter auto tuning technique for these algorithms.

OnlineSTL: Scaling Time Series Decomposition by 100x

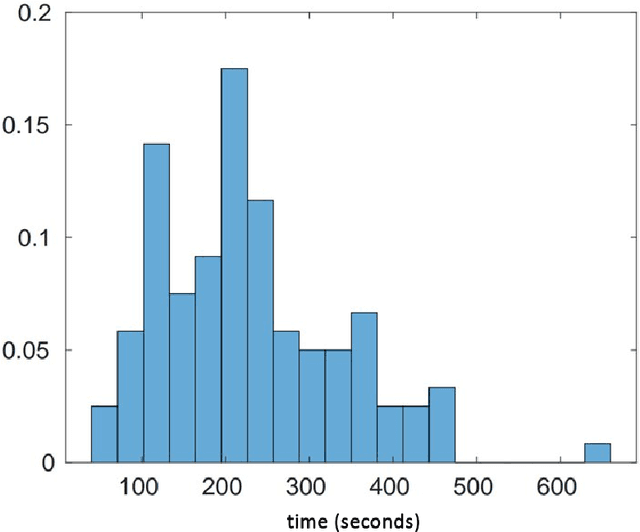
Decomposing a complex time series into trend, seasonality, and remainder components is an important primitive that facilitates time series anomaly detection, change point detection and forecasting. Although numerous batch algorithms are known for time series decomposition, none operate well in an online scalable setting where high throughput and real-time response are paramount. In this paper, we propose OnlineSTL, a novel online algorithm for time series decomposition which solves the scalability problem and is deployed for real-time metrics monitoring on high resolution, high ingest rate data. Experiments on different synthetic and real world time series datasets demonstrate that OnlineSTL achieves orders of magnitude speedups while maintaining quality of decomposition.

Efficient Algorithms for Estimating the Parameters of Mixed Linear Regression Models

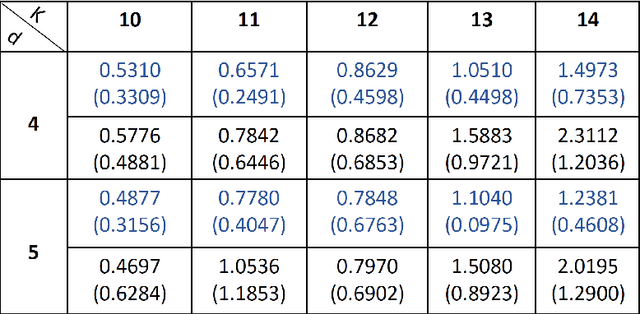
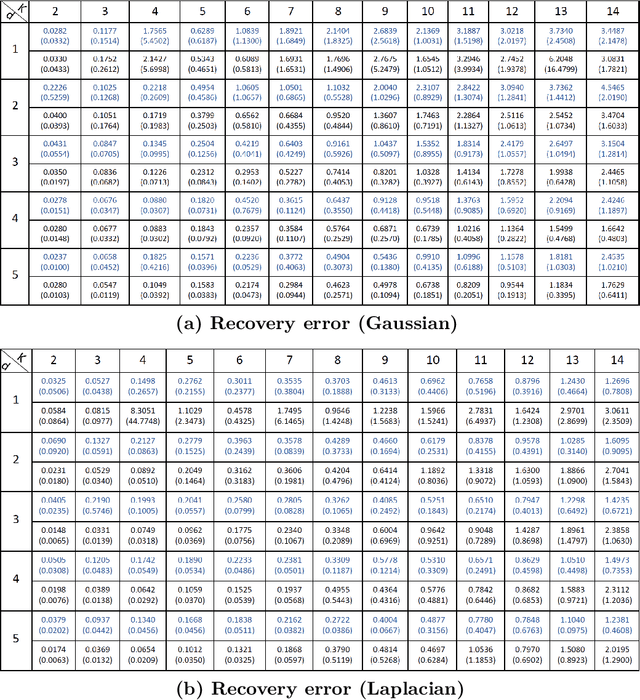
Mixed linear regression (MLR) model is among the most exemplary statistical tools for modeling non-linear distributions using a mixture of linear models. When the additive noise in MLR model is Gaussian, Expectation-Maximization (EM) algorithm is a widely-used algorithm for maximum likelihood estimation of MLR parameters. However, when noise is non-Gaussian, the steps of EM algorithm may not have closed-form update rules, which makes EM algorithm impractical. In this work, we study the maximum likelihood estimation of the parameters of MLR model when the additive noise has non-Gaussian distribution. In particular, we consider the case that noise has Laplacian distribution and we first show that unlike the the Gaussian case, the resulting sub-problems of EM algorithm in this case does not have closed-form update rule, thus preventing us from using EM in this case. To overcome this issue, we propose a new algorithm based on combining the alternating direction method of multipliers (ADMM) with EM algorithm idea. Our numerical experiments show that our method outperforms the EM algorithm in statistical accuracy and computational time in non-Gaussian noise case.

An Algorithm for Online K-Means Clustering

This paper shows that one can be competitive with the k-means objective while operating online. In this model, the algorithm receives vectors v_1,...,v_n one by one in an arbitrary order. For each vector the algorithm outputs a cluster identifier before receiving the next one. Our online algorithm generates ~O(k) clusters whose k-means cost is ~O(W*). Here, W* is the optimal k-means cost using k clusters and ~O suppresses poly-logarithmic factors. We also show that, experimentally, it is not much worse than k-means++ while operating in a strictly more constrained computational model.