A Method for Robust Online Classification using Dictionary Learning: Development and Assessment for Monitoring Manual Material Handling Activities Using Wearable Sensors

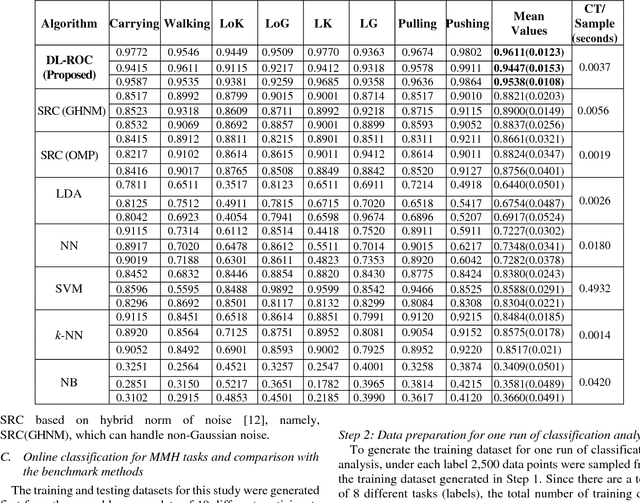
Classification methods based on sparse estimation have drawn much attention recently, due to their effectiveness in processing high-dimensional data such as images. In this paper, a method to improve the performance of a sparse representation classification (SRC) approach is proposed; it is then applied to the problem of online process monitoring of human workers, specifically manual material handling (MMH) operations monitored using wearable sensors (involving 111 sensor channels). Our proposed method optimizes the design matrix (aka dictionary) in the linear model used for SRC, minimizing its ill-posedness to achieve a sparse solution. This procedure is based on the idea of dictionary learning (DL): we optimize the design matrix formed by training datasets to minimize both redundancy and coherency as well as reducing the size of these datasets. Use of such optimized training data can subsequently improve classification accuracy and help decrease the computational time needed for the SRC; it is thus more applicable for online process monitoring. Performance of the proposed methodology is demonstrated using wearable sensor data obtained from manual material handling experiments, and is found to be superior to those of benchmark methods in terms of accuracy, while also requiring computational time appropriate for MMH online monitoring.

On the Use of the Observability Gramian for Partially Observed Robotic Path Planning Problems

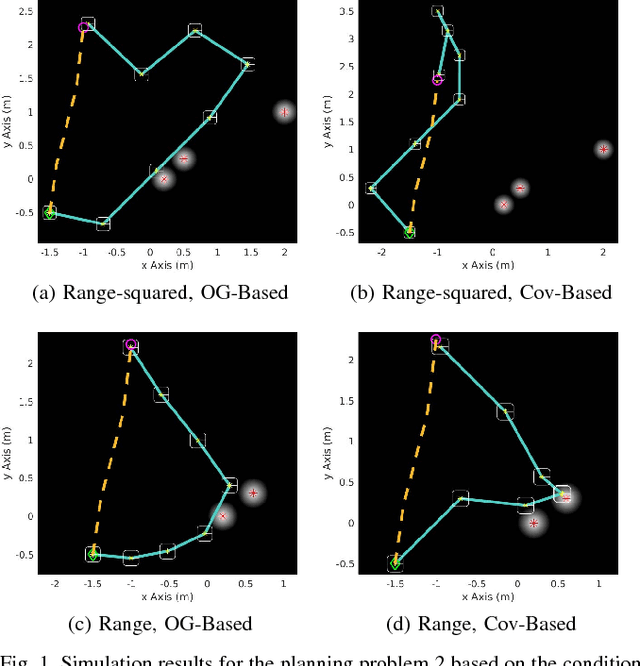
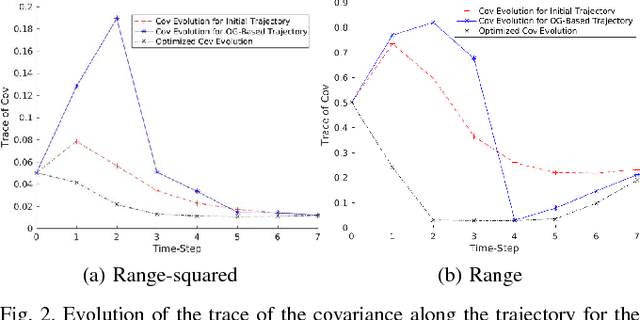
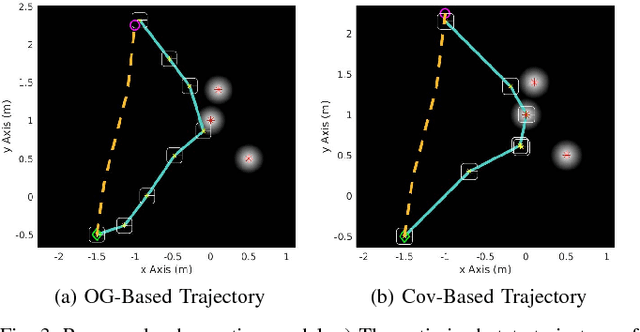
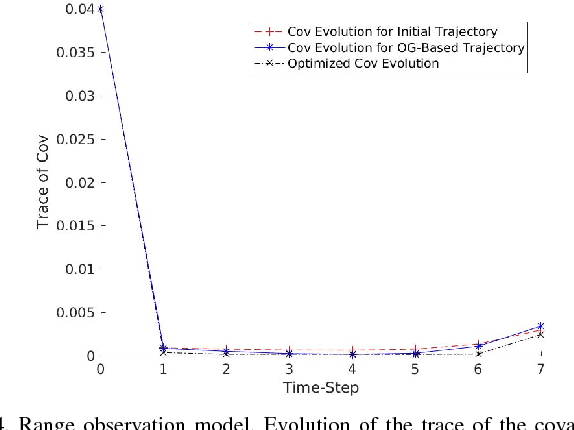
Optimizing measures of the observability Gramian as a surrogate for the estimation performance may provide irrelevant or misleading trajectories for planning under observation uncertainty.

A Separation-Based Design to Data-Driven Control for Large-Scale Partially Observed Systems

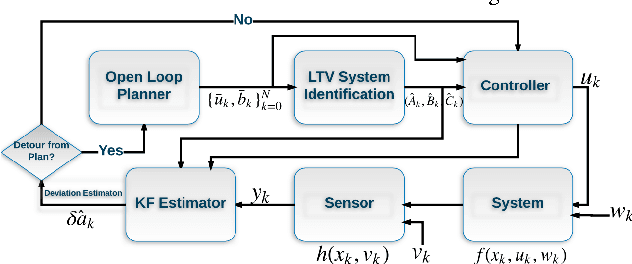
This paper studies the partially observed stochastic optimal control problem for systems with state dynamics governed by Partial Differential Equations (PDEs) that leads to an extremely large problem. First, an open-loop deterministic trajectory optimization problem is solved using a black box simulation model of the dynamical system. Next, a Linear Quadratic Gaussian (LQG) controller is designed for the nominal trajectory-dependent linearized system, which is identified using input-output experimental data consisting of the impulse responses of the optimized nominal system. A computational nonlinear heat example is used to illustrate the performance of the approach.

Near-Optimal Belief Space Planning via T-LQG

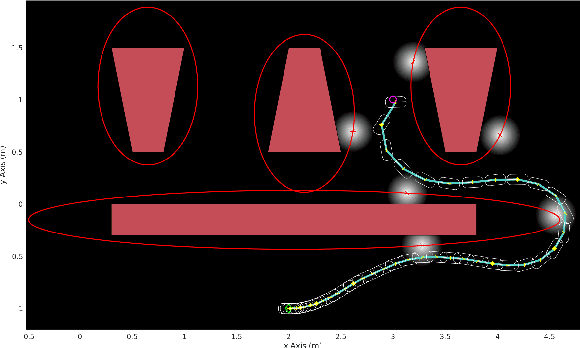
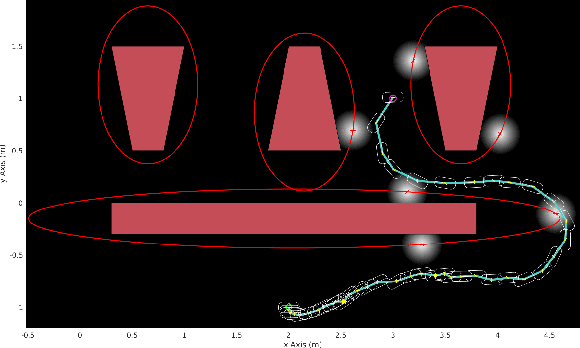
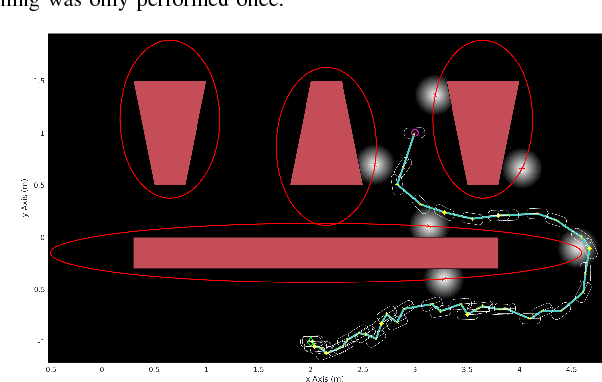
We consider the problem of planning under observation and motion uncertainty for nonlinear robotics systems. Determining the optimal solution to this problem, generally formulated as a Partially Observed Markov Decision Process (POMDP), is computationally intractable. We propose a Trajectory-optimized Linear Quadratic Gaussian (T-LQG) approach that leads to quantifiably near-optimal solutions for the POMDP problem. We provide a novel "separation principle" for the design of an optimal nominal open-loop trajectory followed by an optimal feedback control law, which provides a near-optimal feedback control policy for belief space planning problems involving a polynomial order of calculations of minimum order.

Stochastic Feedback Control of Systems with Unknown Nonlinear Dynamics

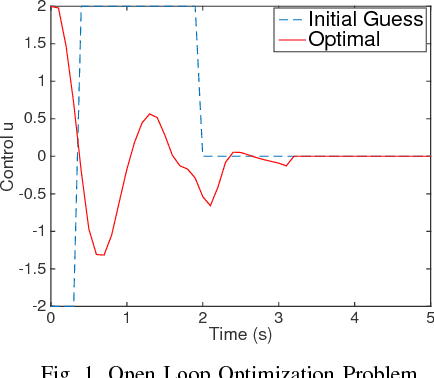
This paper studies the stochastic optimal control problem for systems with unknown dynamics. First, an open-loop deterministic trajectory optimization problem is solved without knowing the explicit form of the dynamical system. Next, a Linear Quadratic Gaussian (LQG) controller is designed for the nominal trajectory-dependent linearized system, such that under a small noise assumption, the actual states remain close to the optimal trajectory. The trajectory-dependent linearized system is identified using input-output experimental data consisting of the impulse responses of the nominal system. A computational example is given to illustrate the performance of the proposed approach.

A Near-Optimal Separation Principle for Nonlinear Stochastic Systems Arising in Robotic Path Planning and Control

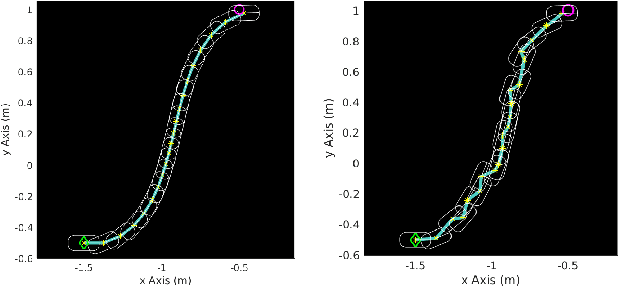
We consider nonlinear stochastic systems that arise in path planning and control of mobile robots. As is typical of almost all nonlinear stochastic systems, the optimally solving problem is intractable. We provide a design approach which yields a tractable design that is quantifiably near-optimal. We exhibit a "separation" principle under a small noise assumption consisting of the optimal open-loop design of nominal trajectory followed by an optimal feedback law to track this trajectory, which is different from the usual effort of separating estimation from control. As a corollary, we obtain a trajectory-optimized linear quadratic regulator design for stochastic nonlinear systems with Gaussian noise.

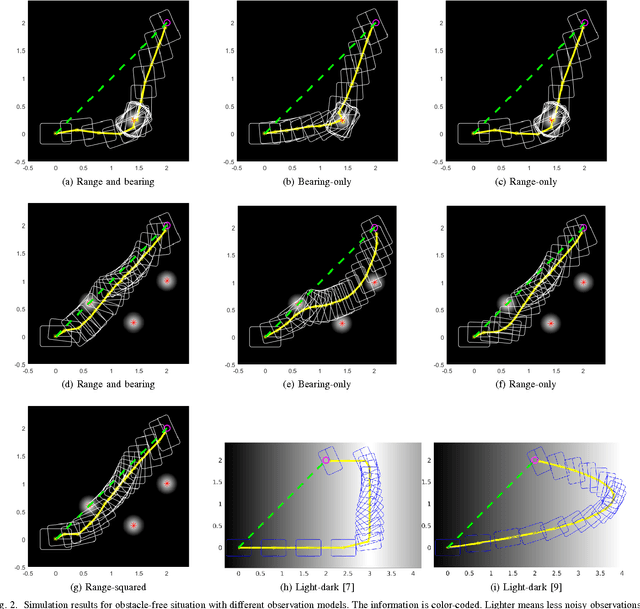
Non-Gaussian SLAP: Simultaneous Localization and Planning Under Non-Gaussian Uncertainty in Static and Dynamic Environments

Simultaneous Localization and Planning (SLAP) under process and measurement uncertainties is a challenge. It involves solving a stochastic control problem modeled as a Partially Observed Markov Decision Process (POMDP) in a general framework. For a convex environment, we propose an optimization-based open-loop optimal control problem coupled with receding horizon control strategy to plan for high quality trajectories along which the uncertainty of the state localization is reduced while the system reaches to a goal state with minimum control effort. In a static environment with non-convex state constraints, the optimization is modified by defining barrier functions to obtain collision-free paths while maintaining the previous goals. By initializing the optimization with trajectories in different homotopy classes and comparing the resultant costs, we improve the quality of the solution in the presence of action and measurement uncertainties. In dynamic environments with time-varying constraints such as moving obstacles or banned areas, the approach is extended to find collision-free trajectories. In this paper, the underlying spaces are continuous, and beliefs are non-Gaussian. Without obstacles, the optimization is a globally convex problem, while in the presence of obstacles it becomes locally convex. We demonstrate the performance of the method on different scenarios.

Belief Space Planning Simplified: Trajectory-Optimized LQG (T-LQG) (Extended Report)

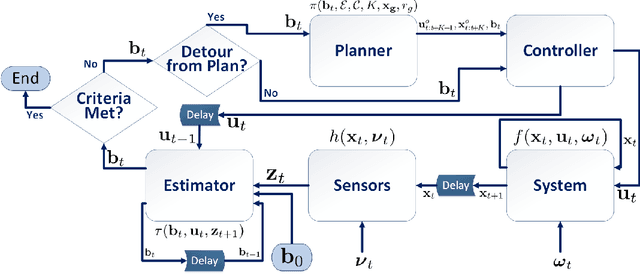
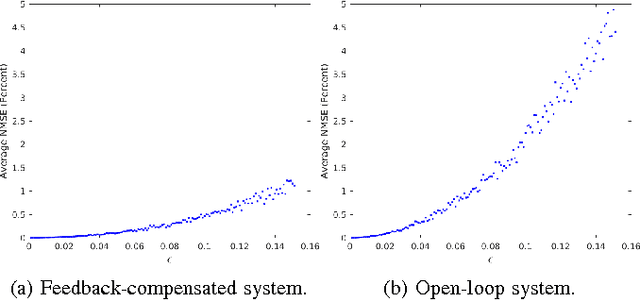
Planning under motion and observation uncertainties requires solution of a stochastic control problem in the space of feedback policies. In this paper, we reduce the general (n^2+n)-dimensional belief space planning problem to an (n)-dimensional problem by obtaining a Linear Quadratic Gaussian (LQG) design with the best nominal performance. Then, by taking the underlying trajectory of the LQG controller as the decision variable, we pose a coupled design of trajectory, estimator, and controller design through a Non-Linear Program (NLP) that can be solved by a general NLP solver. We prove that under a first-order approximation and a careful usage of the separation principle, our approximations are valid. We give an analysis on the existing major belief space planning methods and show that our algorithm has the lowest computational burden. Finally, we extend our solution to contain general state and control constraints. Our simulation results support our design.

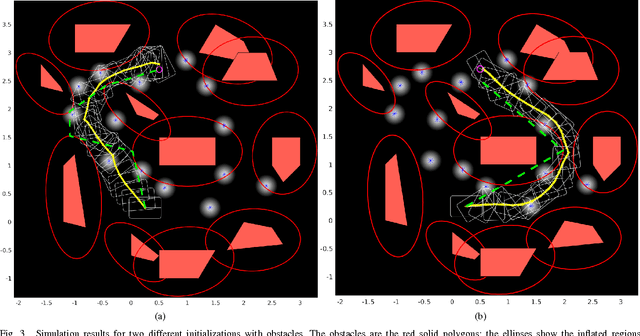
Feedback Motion Planning Under Non-Gaussian Uncertainty and Non-Convex State Constraints

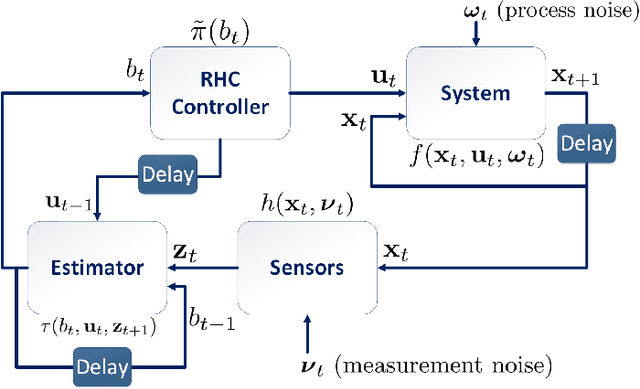
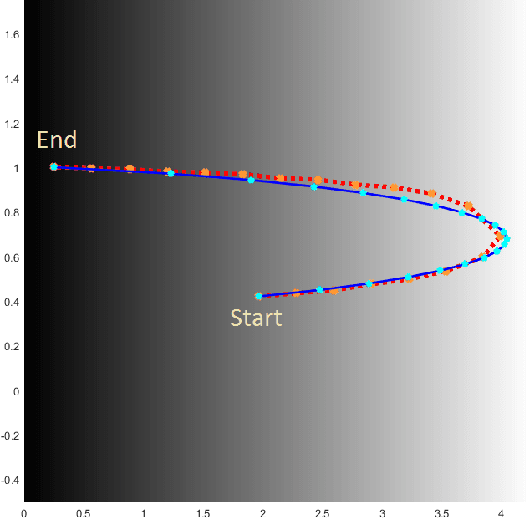
Planning under process and measurement uncertainties is a challenging problem. In its most general form it can be modeled as a Partially Observed Markov Decision Process (POMDP) problem. However POMDPs are generally difficult to solve when the underlying spaces are continuous, particularly when beliefs are non-Gaussian, and the difficulty is further exacerbated when there are also non-convex constraints on states. Existing algorithms to address such challenging POMDPs are expensive in terms of computation and memory. In this paper, we provide a feedback policy in non-Gaussian belief space via solving a convex program for common non-linear observation models. The solution involves a Receding Horizon Control strategy using particle filters for the non-Gaussian belief representation. We develop a way of capturing non-convex constraints in the state space and adapt the optimization to incorporate such constraints, as well. A key advantage of this method is that it does not introduce additional variables in the optimization problem and is therefore more scalable than existing constrained problems in belief space. We demonstrate the performance of the method on different scenarios.