A Near-Optimal Separation Principle for Nonlinear Stochastic Systems Arising in Robotic Path Planning and Control
Paper and Code
May 24, 2017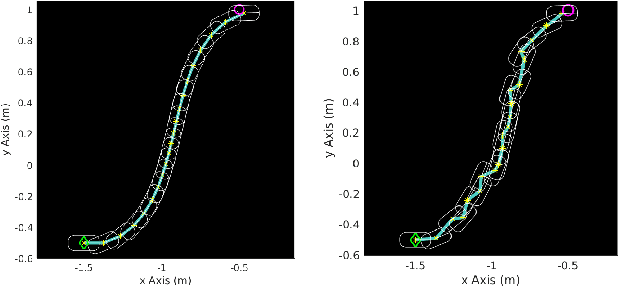
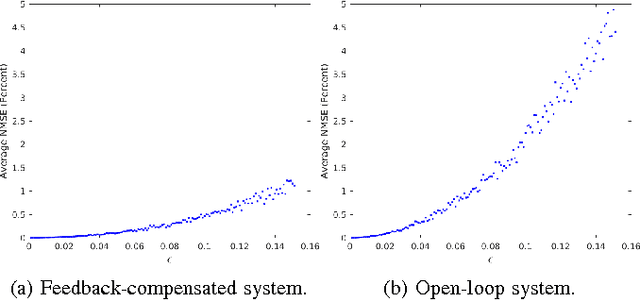
We consider nonlinear stochastic systems that arise in path planning and control of mobile robots. As is typical of almost all nonlinear stochastic systems, the optimally solving problem is intractable. We provide a design approach which yields a tractable design that is quantifiably near-optimal. We exhibit a "separation" principle under a small noise assumption consisting of the optimal open-loop design of nominal trajectory followed by an optimal feedback law to track this trajectory, which is different from the usual effort of separating estimation from control. As a corollary, we obtain a trajectory-optimized linear quadratic regulator design for stochastic nonlinear systems with Gaussian noise.
* 7 pages, 4 Figures, Submitted to 56th IEEE Conference on Decision and
Control (CDC), 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge