Learning to Control under Uncertainty with Data-Based Iterative Linear Quadratic Regulator

This paper studies the learning-to-control problem under process and sensing uncertainties for dynamical systems. In our previous work, we developed a data-based generalization of the iterative linear quadratic regulator (iLQR) to design closed-loop feedback control for high-dimensional dynamical systems with partial state observation. This method required perfect simulation rollouts which are not realistic in real applications. In this work, we briefly introduce this method and explore its efficacy under process and sensing uncertainties. We prove that in the fully observed case where the system dynamics are corrupted with noise but the measurements are perfect, it still converges to the global minimum. However, in the partially observed case where both process and measurement noise exist in the system, this method converges to a biased "optimum". Thus multiple rollouts need to be averaged to retrieve the true optimum. The analysis is verified in two nonlinear robotic examples simulated in the above cases.

Partially-Observed Decoupled Data-based Control (POD2C) for Complex Robotic Systems

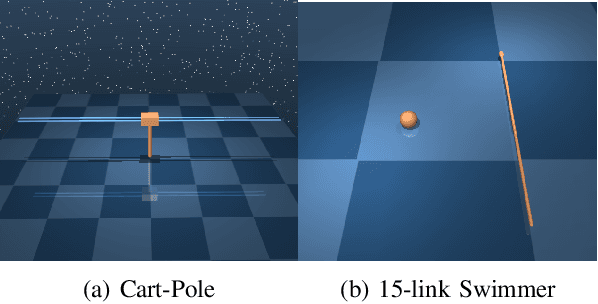
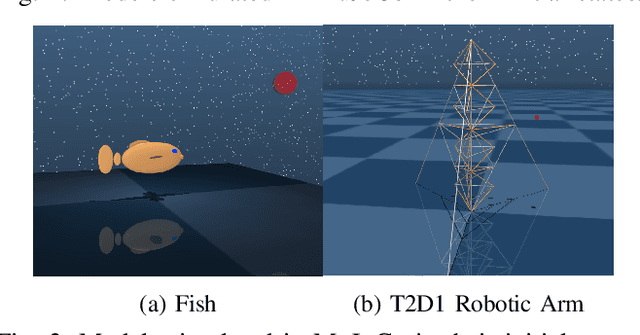
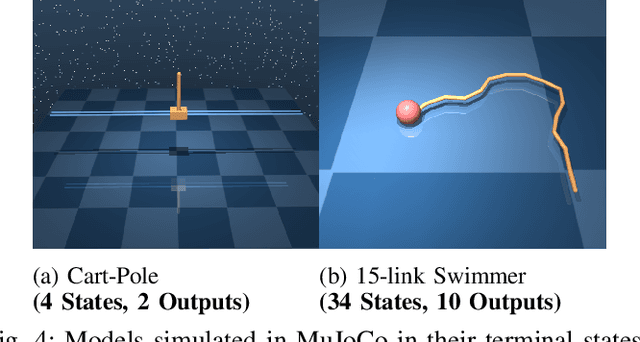
This paper develops a systematic data-based approach to the closed-loop feedback control of high-dimensional robotic systems using only partial state observation. We first develop a model-free generalization of the iterative Linear Quadratic Regulator (iLQR) to partially-observed systems using an Autoregressive Moving Average (ARMA) model, that is generated using only the input-output data. The ARMA model results in an information state, which has dimension less than or equal to the underlying actual state dimension. This open-loop trajectory optimization solution is then used to design a local feedback control law, and the composite law then provides a solution to the partially observed feedback design problem. The efficacy of the developed method is shown by controlling complex high dimensional nonlinear robotic systems in the presence of model and sensing uncertainty and for which analytical models are either unavailable or inaccurate.

On the Convergence of Reinforcement Learning

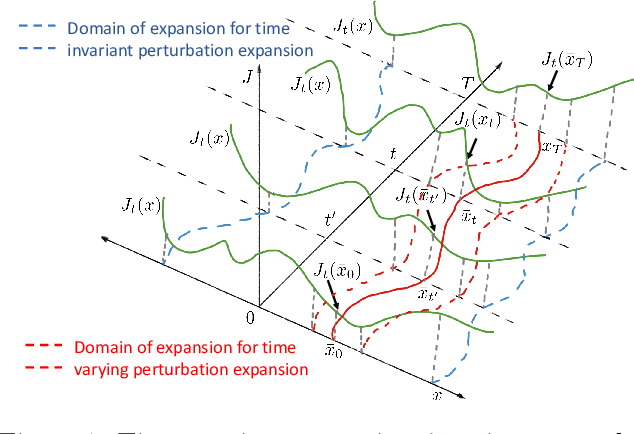
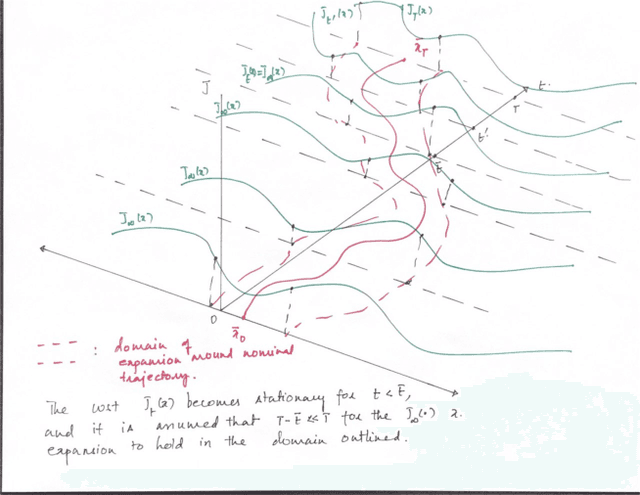
We consider the problem of Reinforcement Learning for nonlinear stochastic dynamical systems. We show that in the RL setting, there is an inherent "Curse of Variance" in addition to Bellman's infamous "Curse of Dimensionality", in particular, we show that the variance in the solution grows factorial-exponentially in the order of the approximation. A fundamental consequence is that this precludes the search for anything other than "local" feedback solutions in RL, in order to control the explosive variance growth, and thus, ensure accuracy. We further show that the deterministic optimal control has a perturbation structure, in that the higher order terms do not affect the calculation of lower order terms, which can be utilized in RL to get accurate local solutions.

Near Optimality and Tractability in Stochastic Nonlinear Control

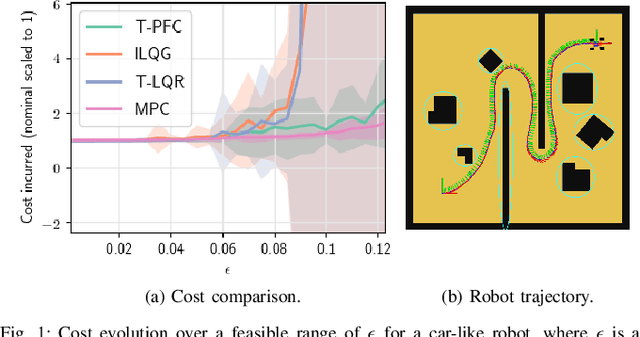
We consider the problem of nonlinear stochastic optimal control. This is fundamentally intractable owing to Bellman's infamous "curse of dimensionality". We present a "decoupling principle" for the tractable feedback design for such problems, wherein, first, a nominal open-loop problem is solved, followed by a suitable linear feedback design around the open-loop. The performance of the resulting feedback law is shown to be asymptotically close to the true stochastic feedback law to fourth order in a small noise parameter $\epsilon$. The decoupling theory is empirically tested on robotic planning problems under uncertainty.

On the Search for Feedback in Reinforcement Learning

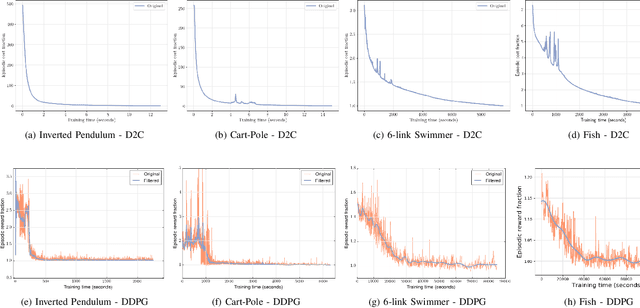
This paper addresses the problem of learning the optimal feedback policy for a nonlinear stochastic dynamical system with continuous state space, continuous action space and unknown dynamics. Feedback policies are complex objects that typically need a large dimensional parametrization, which makes Reinforcement Learning algorithms that search for an optimum in this large parameter space, sample inefficient and subject to high variance. We propose a "decoupling" principle that drastically reduces the feedback parameter space while still remaining near-optimal to the fourth-order in a small noise parameter. Based on this principle, we propose a decoupled data-based control (D2C) algorithm that addresses the stochastic control problem: first, an open-loop deterministic trajectory optimization problem is solved using a black-box simulation model of the dynamical system. Then, a linear closed-loop control is developed around this nominal trajectory using only a simulation model. Empirical evidence suggests significant reduction in training time, as well as the training variance, compared to other state of the art Reinforcement Learning algorithms.

Experiments with Tractable Feedback in Robotic Planning under Uncertainty: Insights over a wide range of noise regimes

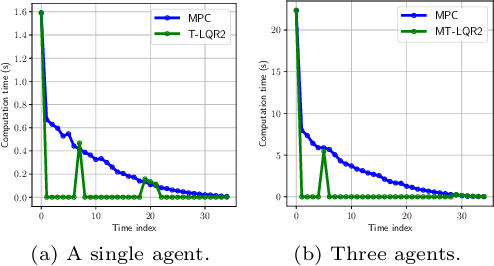
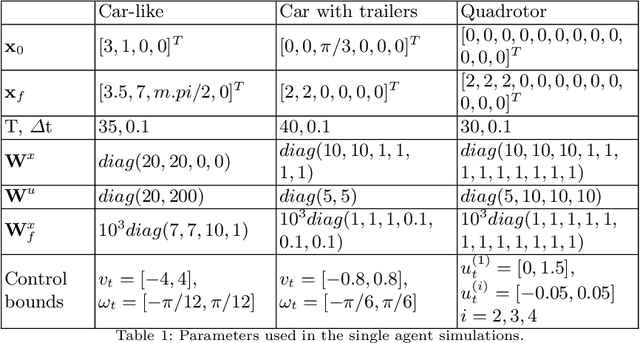
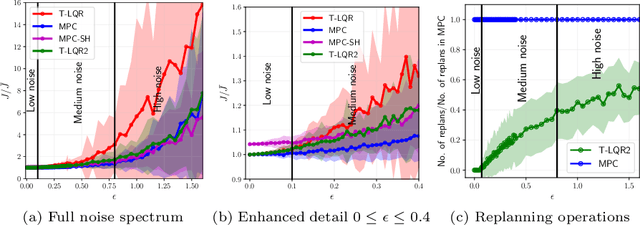
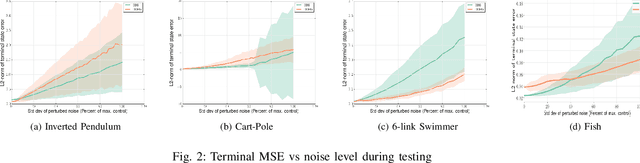
We consider the problem of robotic planning under uncertainty. This problem may be posed as a stochastic optimal control problem, complete solution to which is fundamentally intractable owing to the infamous curse of dimensionality. We report the results of an extensive simulation study in which we have compared two methods, both of which aim to salvage tractability by using alternative, albeit inexact, means for treating feedback. The first is a recently proposed method based on a near-optimal "decoupling principle" for tractable feedback design, wherein a nominal open-loop problem is solved, followed by a linear feedback design around the open-loop. The second is Model Predictive Control (MPC), a widely-employed method that uses repeated re-computation of the nominal open-loop problem during execution to correct for noise, though when interpreted as feedback, this can only said to be an implicit form. We examine a much wider range of noise levels than have been previously reported and empirical evidence suggests that the decoupling method allows for tractable planning over a wide range of uncertainty conditions without unduly sacrificing performance.

D2C 2.0: Decoupled Data-Based Approach for Learning to Control Stochastic Nonlinear Systems via Model-Free ILQR

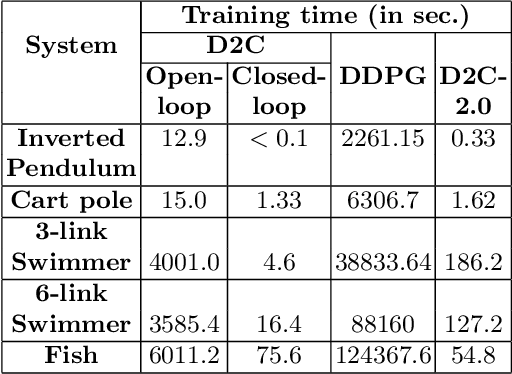
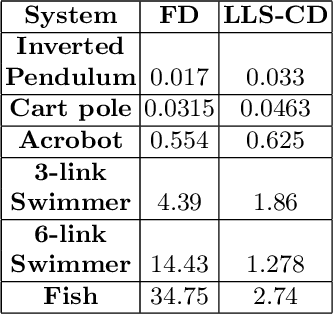
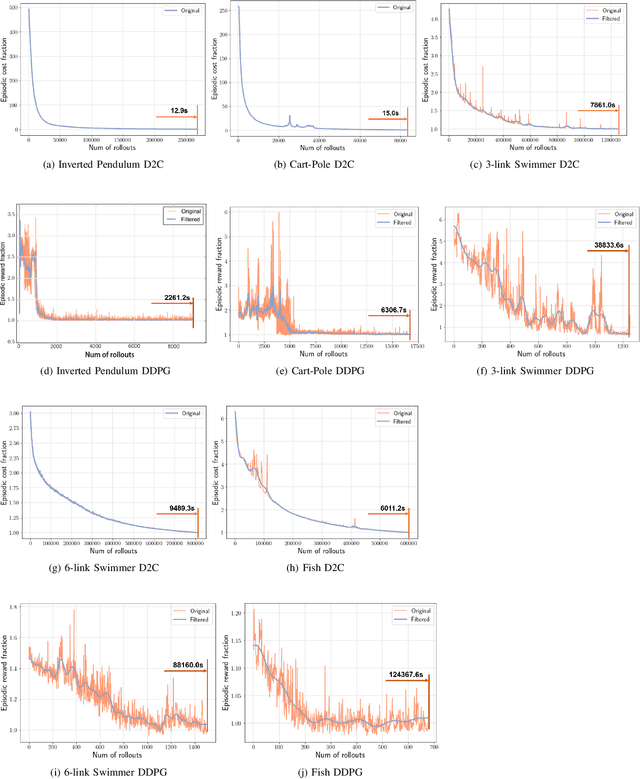
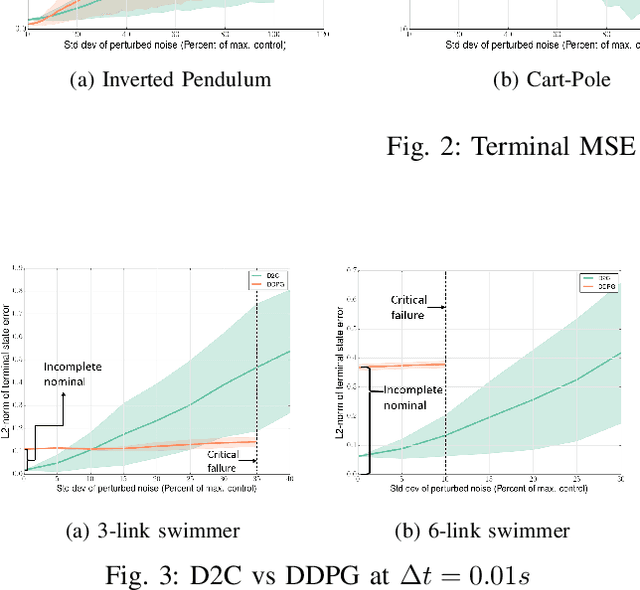
In this paper, we propose a structured linear parameterization of a feedback policy to solve the model-free stochastic optimal control problem. This parametrization is corroborated by a decoupling principle that is shown to be near-optimal under a small noise assumption, both in theory and by empirical analyses. Further, we incorporate a model-free version of the Iterative Linear Quadratic Regulator (ILQR) in a sample-efficient manner into our framework. Simulations on systems over a range of complexities reveal that the resulting algorithm is able to harness the superior second-order convergence properties of ILQR. As a result, it is fast and is scalable to a wide variety of higher dimensional systems. Comparisons are made with a state-of-the-art reinforcement learning algorithm, the Deep Deterministic Policy Gradient (DDPG) technique, in order to demonstrate the significant merits of our approach in terms of training-efficiency.

Decoupled Data Based Approach for Learning to Control Nonlinear Dynamical Systems

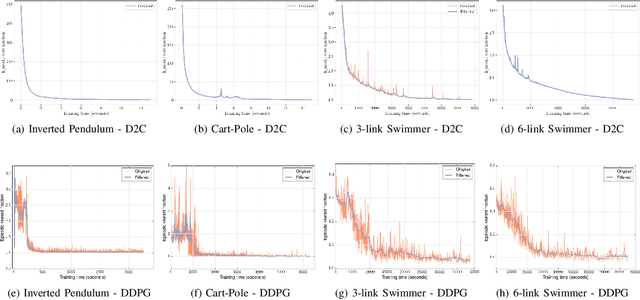
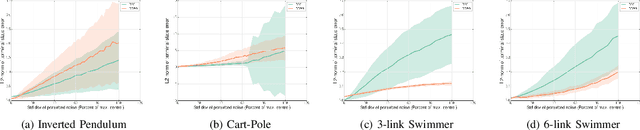
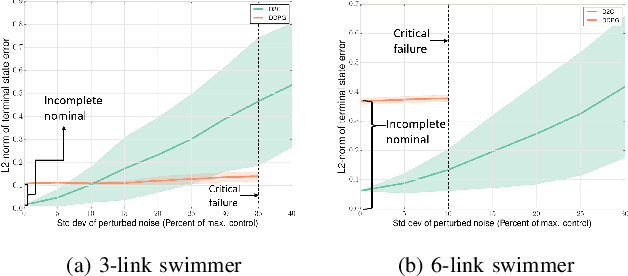
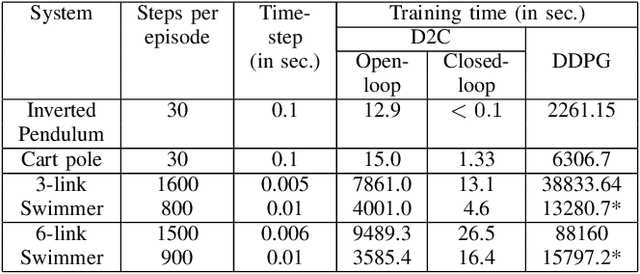
This paper addresses the problem of learning the optimal control policy for a nonlinear stochastic dynamical system with continuous state space, continuous action space and unknown dynamics. This class of problems are typically addressed in stochastic adaptive control and reinforcement learning literature using model-based and model-free approaches respectively. Both methods rely on solving a dynamic programming problem, either directly or indirectly, for finding the optimal closed loop control policy. The inherent `curse of dimensionality' associated with dynamic programming method makes these approaches also computationally difficult. This paper proposes a novel decoupled data-based control (D2C) algorithm that addresses this problem using a decoupled, `open loop - closed loop', approach. First, an open-loop deterministic trajectory optimization problem is solved using a black-box simulation model of the dynamical system. Then, a closed loop control is developed around this open loop trajectory by linearization of the dynamics about this nominal trajectory. By virtue of linearization, a linear quadratic regulator based algorithm can be used for this closed loop control. We show that the performance of D2C algorithm is approximately optimal. Moreover, simulation performance suggests significant reduction in training time compared to other state of the art algorithms.

SLAP: Simultaneous Localization and Planning Under Uncertainty for Physical Mobile Robots via Dynamic Replanning in Belief Space: Extended version

Simultaneous localization and Planning (SLAP) is a crucial ability for an autonomous robot operating under uncertainty. In its most general form, SLAP induces a continuous POMDP (partially-observable Markov decision process), which needs to be repeatedly solved online. This paper addresses this problem and proposes a dynamic replanning scheme in belief space. The underlying POMDP, which is continuous in state, action, and observation space, is approximated offline via sampling-based methods, but operates in a replanning loop online to admit local improvements to the coarse offline policy. This construct enables the proposed method to combat changing environments and large localization errors, even when the change alters the homotopy class of the optimal trajectory. It further outperforms the state-of-the-art FIRM (Feedback-based Information RoadMap) method by eliminating unnecessary stabilization steps. Applying belief space planning to physical systems brings with it a plethora of challenges. A key focus of this paper is to implement the proposed planner on a physical robot and show the SLAP solution performance under uncertainty, in changing environments and in the presence of large disturbances, such as a kidnapped robot situation.

On the Use of the Observability Gramian for Partially Observed Robotic Path Planning Problems

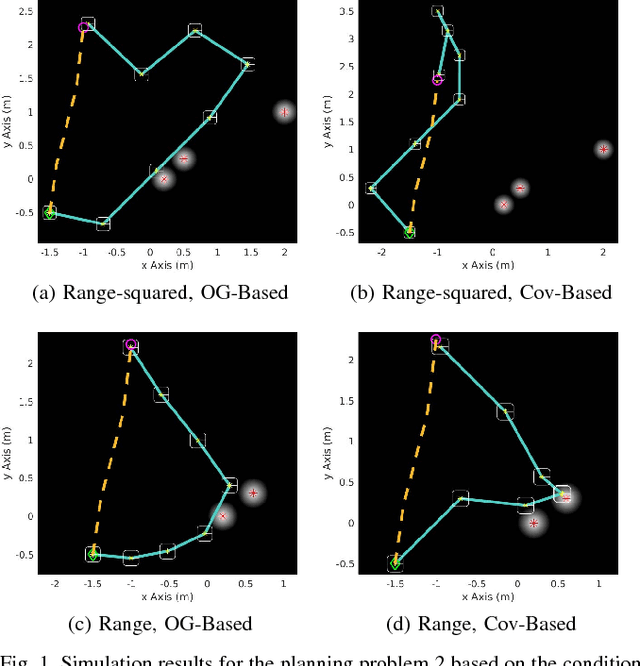
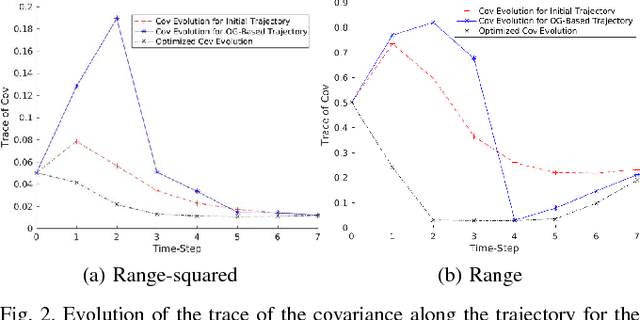
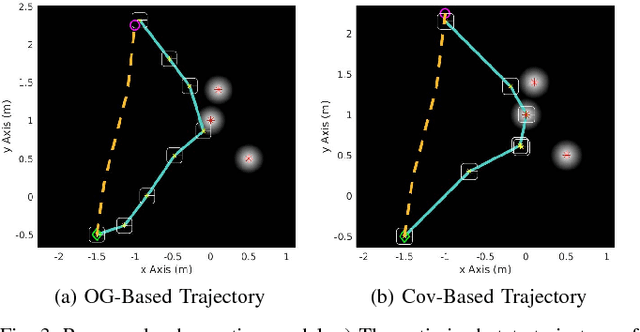
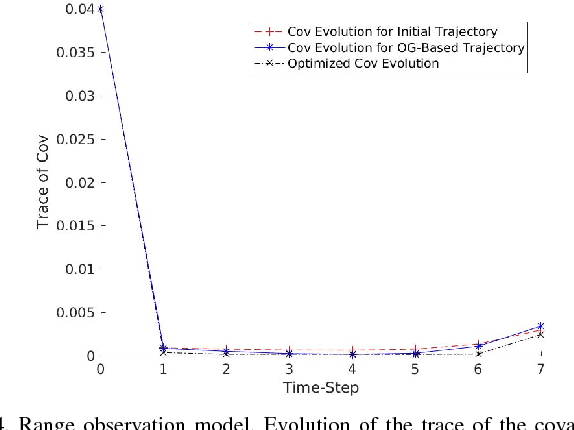
Optimizing measures of the observability Gramian as a surrogate for the estimation performance may provide irrelevant or misleading trajectories for planning under observation uncertainty.