Decoupled Data Based Approach for Learning to Control Nonlinear Dynamical Systems
Paper and Code
Apr 17, 2019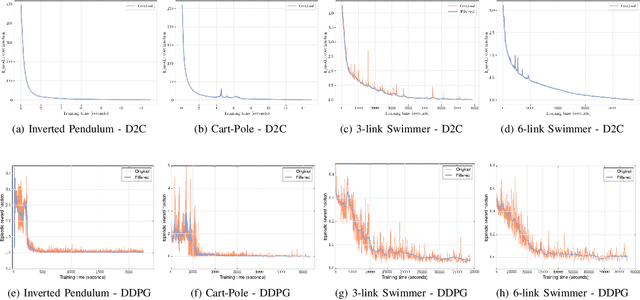
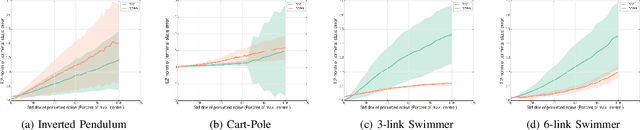
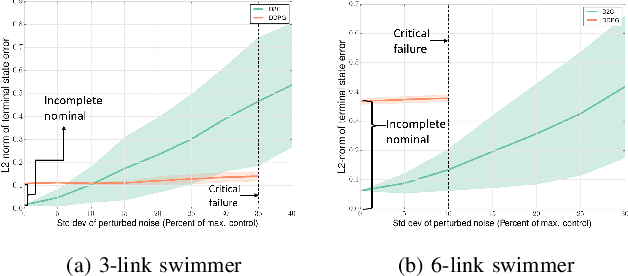
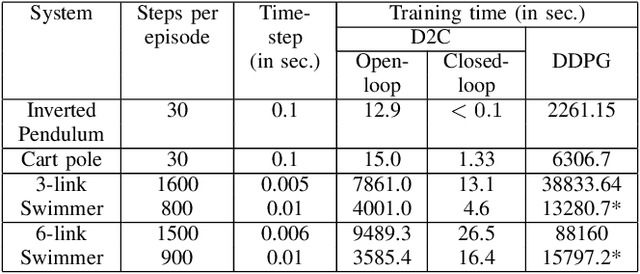
This paper addresses the problem of learning the optimal control policy for a nonlinear stochastic dynamical system with continuous state space, continuous action space and unknown dynamics. This class of problems are typically addressed in stochastic adaptive control and reinforcement learning literature using model-based and model-free approaches respectively. Both methods rely on solving a dynamic programming problem, either directly or indirectly, for finding the optimal closed loop control policy. The inherent `curse of dimensionality' associated with dynamic programming method makes these approaches also computationally difficult. This paper proposes a novel decoupled data-based control (D2C) algorithm that addresses this problem using a decoupled, `open loop - closed loop', approach. First, an open-loop deterministic trajectory optimization problem is solved using a black-box simulation model of the dynamical system. Then, a closed loop control is developed around this open loop trajectory by linearization of the dynamics about this nominal trajectory. By virtue of linearization, a linear quadratic regulator based algorithm can be used for this closed loop control. We show that the performance of D2C algorithm is approximately optimal. Moreover, simulation performance suggests significant reduction in training time compared to other state of the art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge