Karthikeya S Parunandi
D2C 2.0: Decoupled Data-Based Approach for Learning to Control Stochastic Nonlinear Systems via Model-Free ILQR
Feb 18, 2020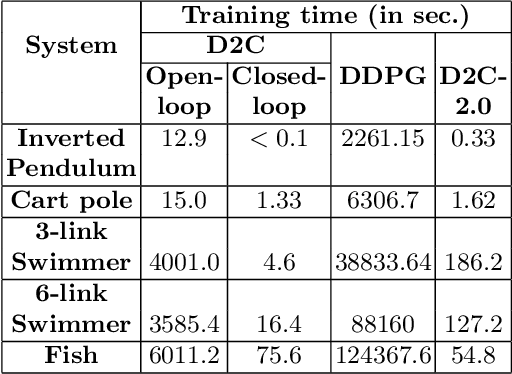


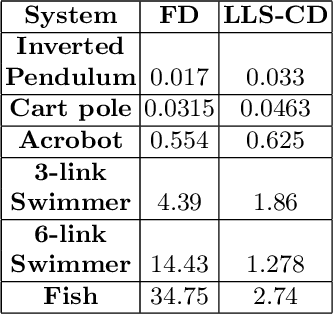
Abstract:In this paper, we propose a structured linear parameterization of a feedback policy to solve the model-free stochastic optimal control problem. This parametrization is corroborated by a decoupling principle that is shown to be near-optimal under a small noise assumption, both in theory and by empirical analyses. Further, we incorporate a model-free version of the Iterative Linear Quadratic Regulator (ILQR) in a sample-efficient manner into our framework. Simulations on systems over a range of complexities reveal that the resulting algorithm is able to harness the superior second-order convergence properties of ILQR. As a result, it is fast and is scalable to a wide variety of higher dimensional systems. Comparisons are made with a state-of-the-art reinforcement learning algorithm, the Deep Deterministic Policy Gradient (DDPG) technique, in order to demonstrate the significant merits of our approach in terms of training-efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge