On the Convergence of Reinforcement Learning

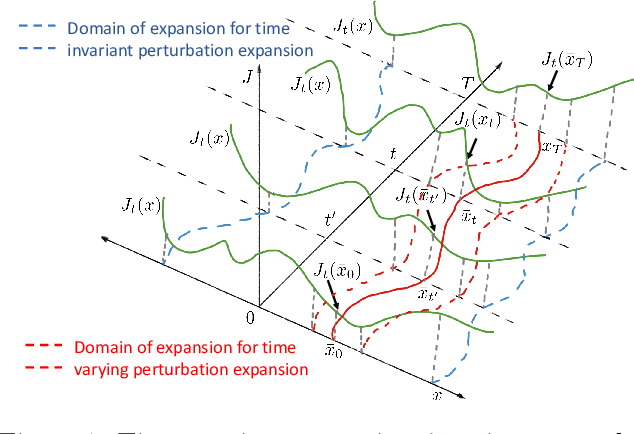
We consider the problem of Reinforcement Learning for nonlinear stochastic dynamical systems. We show that in the RL setting, there is an inherent "Curse of Variance" in addition to Bellman's infamous "Curse of Dimensionality", in particular, we show that the variance in the solution grows factorial-exponentially in the order of the approximation. A fundamental consequence is that this precludes the search for anything other than "local" feedback solutions in RL, in order to control the explosive variance growth, and thus, ensure accuracy. We further show that the deterministic optimal control has a perturbation structure, in that the higher order terms do not affect the calculation of lower order terms, which can be utilized in RL to get accurate local solutions.

Near Optimality and Tractability in Stochastic Nonlinear Control

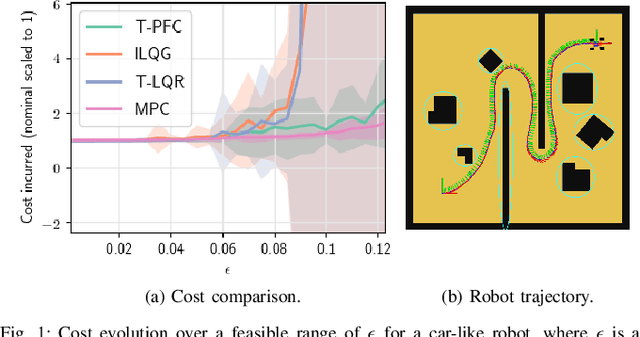
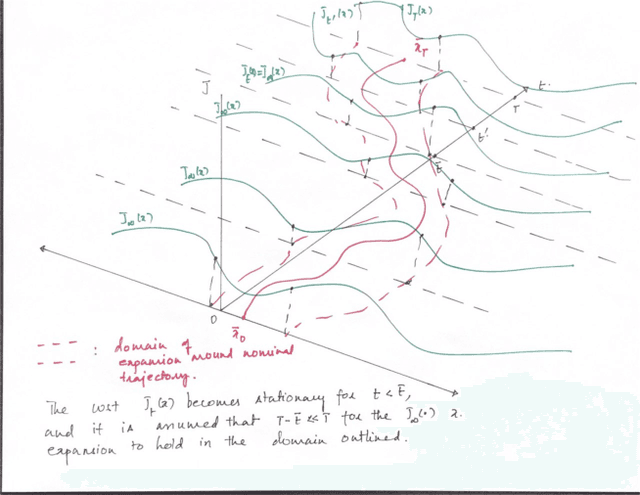
We consider the problem of nonlinear stochastic optimal control. This is fundamentally intractable owing to Bellman's infamous "curse of dimensionality". We present a "decoupling principle" for the tractable feedback design for such problems, wherein, first, a nominal open-loop problem is solved, followed by a suitable linear feedback design around the open-loop. The performance of the resulting feedback law is shown to be asymptotically close to the true stochastic feedback law to fourth order in a small noise parameter $\epsilon$. The decoupling theory is empirically tested on robotic planning problems under uncertainty.

Experiments with Tractable Feedback in Robotic Planning under Uncertainty: Insights over a wide range of noise regimes

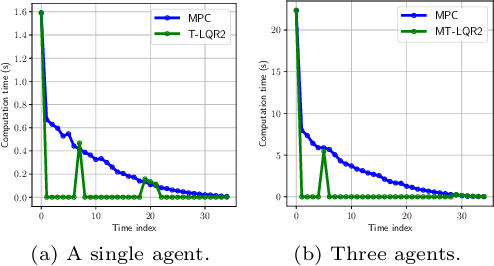
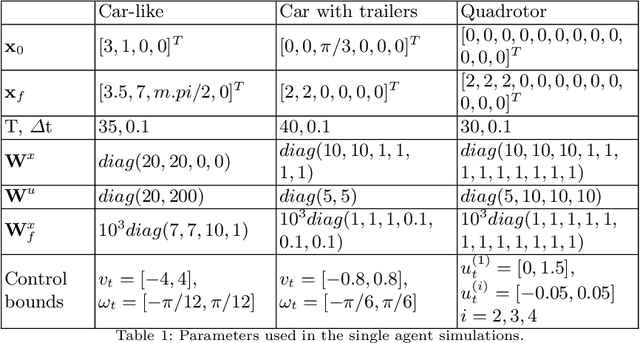
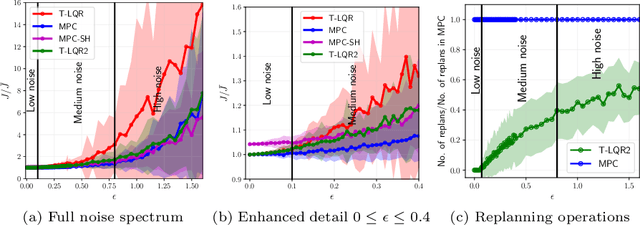
We consider the problem of robotic planning under uncertainty. This problem may be posed as a stochastic optimal control problem, complete solution to which is fundamentally intractable owing to the infamous curse of dimensionality. We report the results of an extensive simulation study in which we have compared two methods, both of which aim to salvage tractability by using alternative, albeit inexact, means for treating feedback. The first is a recently proposed method based on a near-optimal "decoupling principle" for tractable feedback design, wherein a nominal open-loop problem is solved, followed by a linear feedback design around the open-loop. The second is Model Predictive Control (MPC), a widely-employed method that uses repeated re-computation of the nominal open-loop problem during execution to correct for noise, though when interpreted as feedback, this can only said to be an implicit form. We examine a much wider range of noise levels than have been previously reported and empirical evidence suggests that the decoupling method allows for tractable planning over a wide range of uncertainty conditions without unduly sacrificing performance.