On the Convergence of Reinforcement Learning

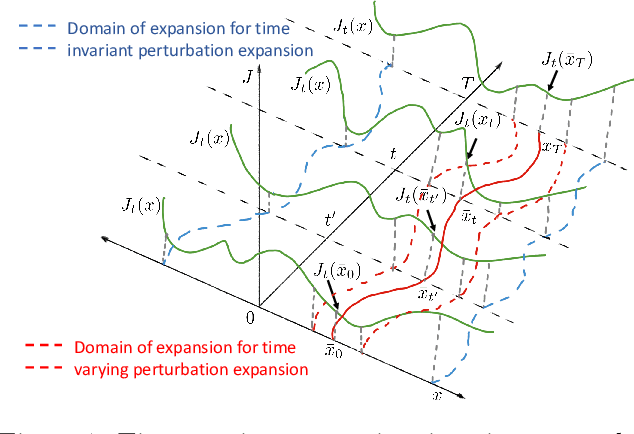
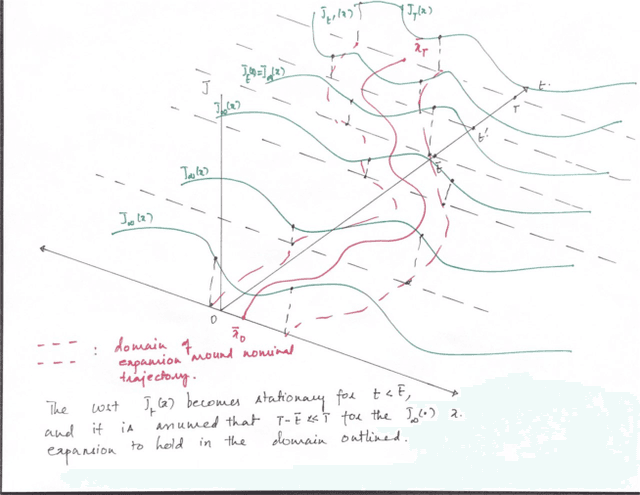
We consider the problem of Reinforcement Learning for nonlinear stochastic dynamical systems. We show that in the RL setting, there is an inherent "Curse of Variance" in addition to Bellman's infamous "Curse of Dimensionality", in particular, we show that the variance in the solution grows factorial-exponentially in the order of the approximation. A fundamental consequence is that this precludes the search for anything other than "local" feedback solutions in RL, in order to control the explosive variance growth, and thus, ensure accuracy. We further show that the deterministic optimal control has a perturbation structure, in that the higher order terms do not affect the calculation of lower order terms, which can be utilized in RL to get accurate local solutions.