Near Optimality and Tractability in Stochastic Nonlinear Control
Paper and Code
Apr 01, 2020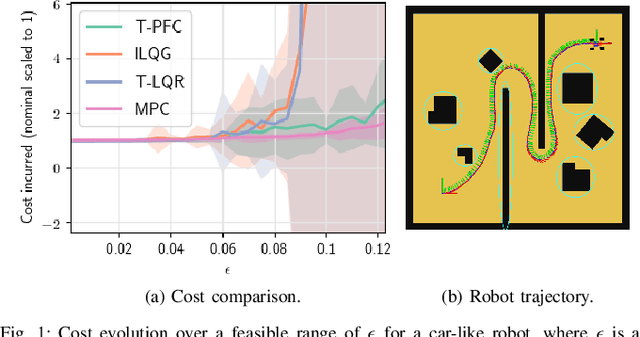
We consider the problem of nonlinear stochastic optimal control. This is fundamentally intractable owing to Bellman's infamous "curse of dimensionality". We present a "decoupling principle" for the tractable feedback design for such problems, wherein, first, a nominal open-loop problem is solved, followed by a suitable linear feedback design around the open-loop. The performance of the resulting feedback law is shown to be asymptotically close to the true stochastic feedback law to fourth order in a small noise parameter $\epsilon$. The decoupling theory is empirically tested on robotic planning problems under uncertainty.
* arXiv admin note: substantial text overlap with arXiv:2002.10505,
arXiv:2002.09478
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge