Partially-Observed Decoupled Data-based Control (POD2C) for Complex Robotic Systems

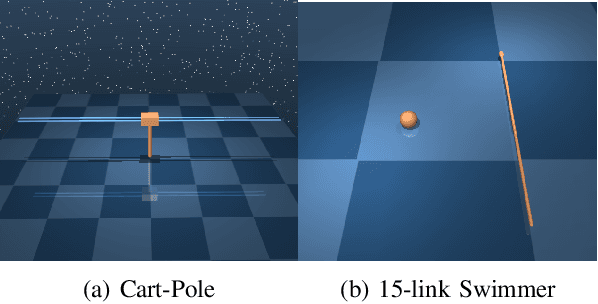
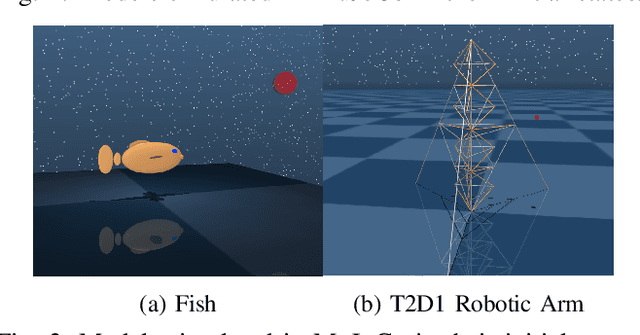
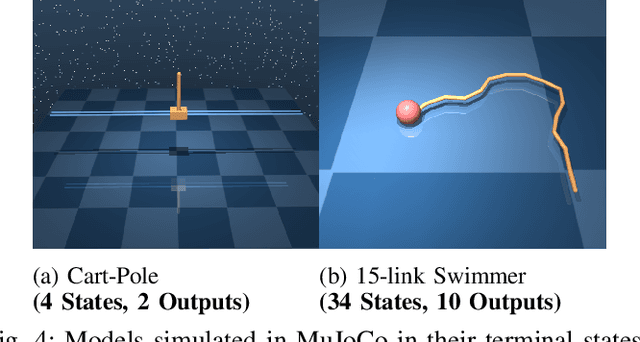
This paper develops a systematic data-based approach to the closed-loop feedback control of high-dimensional robotic systems using only partial state observation. We first develop a model-free generalization of the iterative Linear Quadratic Regulator (iLQR) to partially-observed systems using an Autoregressive Moving Average (ARMA) model, that is generated using only the input-output data. The ARMA model results in an information state, which has dimension less than or equal to the underlying actual state dimension. This open-loop trajectory optimization solution is then used to design a local feedback control law, and the composite law then provides a solution to the partially observed feedback design problem. The efficacy of the developed method is shown by controlling complex high dimensional nonlinear robotic systems in the presence of model and sensing uncertainty and for which analytical models are either unavailable or inaccurate.

Model-based Shape Control of Tensegrity Robotic Systems

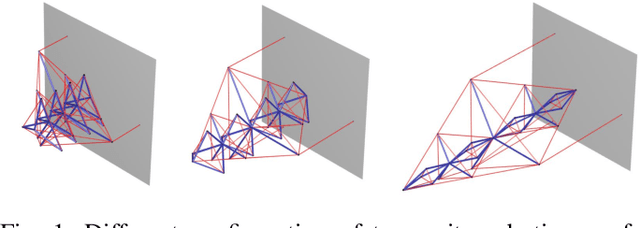
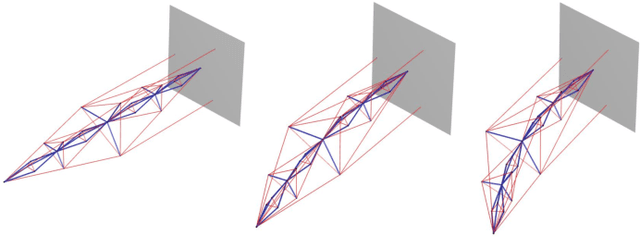
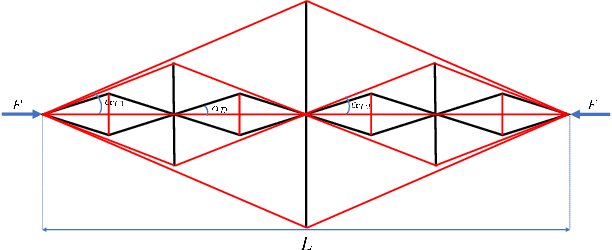
This paper proposes a model-based approach to control the shape of a tensegrity system by driving its node position locations. The nonlinear dynamics of the tensegrity system is used to regulate position, velocity, and acceleration to the specified reference trajectory. State feedback control design is used to obtain the solution for the control variable as a linear programming problem. Shape control for the gyroscopic tensegrity systems is discussed, and it is observed that these systems increase the reachable space for the structure by providing independent control over certain rotational degrees of freedom. Disturbance rejection of the tensegrity system is further studied in the paper. A methodology to calculate the control gains to bound the errors for five different types of problems is provided. The formulation uses a Linear Matrix Inequality (LMI) approach to stipulate the desired performance bounds on the error for $\mathcal{H}_\infty$, generalized $\mathcal{H}_2$, LQR, covariance control and stabilizing control problem. A high degree of freedom tensegrity $T_2D_1$ robotic arm is used as an example to show the efficacy of the formulation.

Markov Data-Based Reference Tracking of Tensegrity Morphing Airfoils

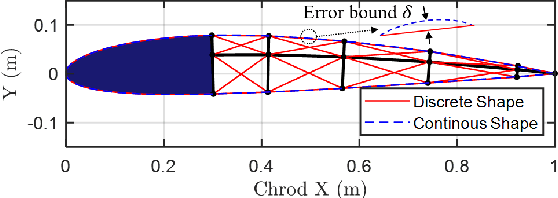
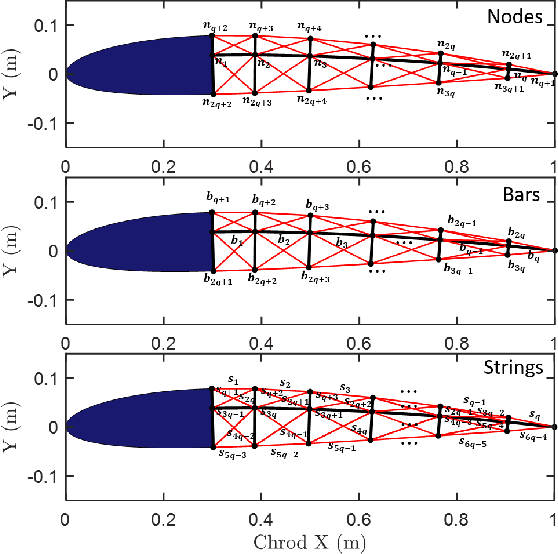
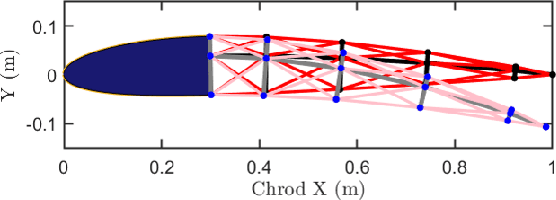
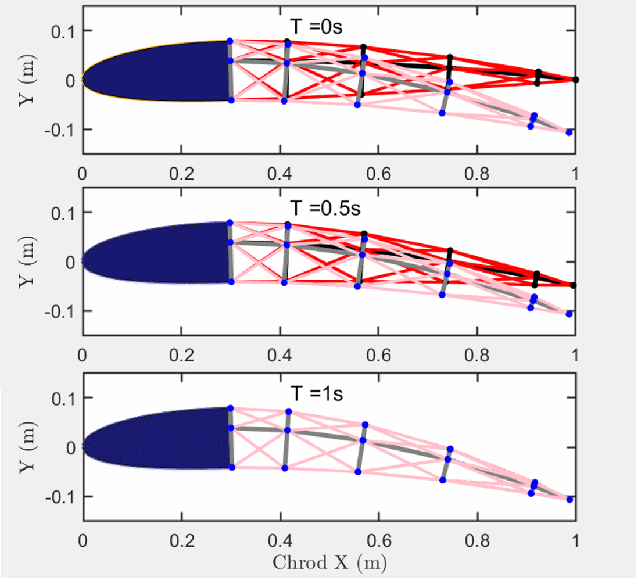
This letter presents a data-based control design for reference tracking applications. This design finds the optimal control sequence, which minimizes a quadratic cost function consisting of tracking error and input increments over a finite interval [0,N]. The only information needed is the first N+1 Markov parameters of the system. This design is employed on a tensegrity morphing airfoil whose topology has been described in detail in this letter. A NACA 2412 airfoil with specified morphing targets is chosen to verify the developed design. The principle developed in this letter is also applicable to other structural control problems.