Model-based Shape Control of Tensegrity Robotic Systems

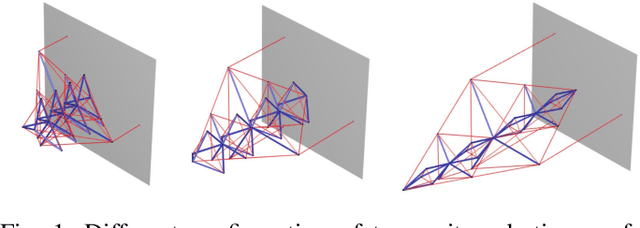
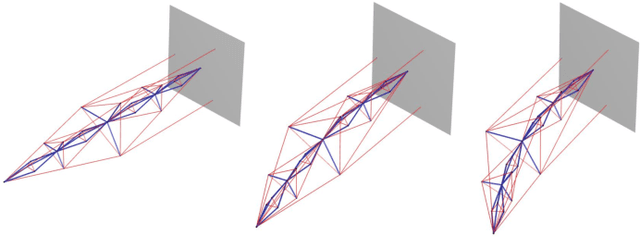
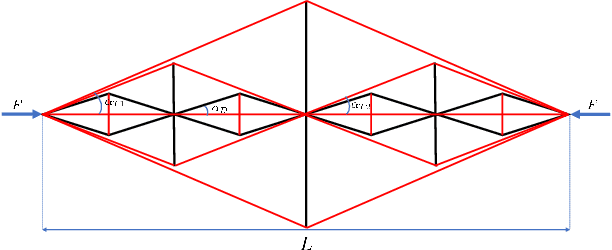
This paper proposes a model-based approach to control the shape of a tensegrity system by driving its node position locations. The nonlinear dynamics of the tensegrity system is used to regulate position, velocity, and acceleration to the specified reference trajectory. State feedback control design is used to obtain the solution for the control variable as a linear programming problem. Shape control for the gyroscopic tensegrity systems is discussed, and it is observed that these systems increase the reachable space for the structure by providing independent control over certain rotational degrees of freedom. Disturbance rejection of the tensegrity system is further studied in the paper. A methodology to calculate the control gains to bound the errors for five different types of problems is provided. The formulation uses a Linear Matrix Inequality (LMI) approach to stipulate the desired performance bounds on the error for $\mathcal{H}_\infty$, generalized $\mathcal{H}_2$, LQR, covariance control and stabilizing control problem. A high degree of freedom tensegrity $T_2D_1$ robotic arm is used as an example to show the efficacy of the formulation.