On the Search for Feedback in Reinforcement Learning
Paper and Code
Feb 21, 2020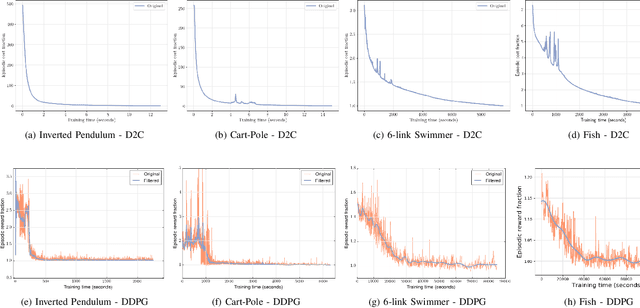
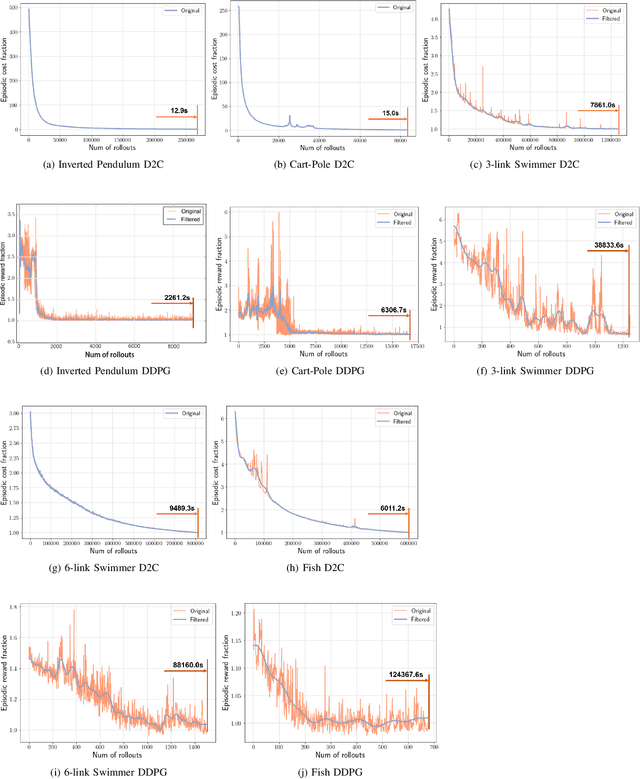
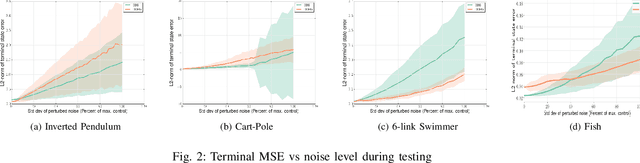
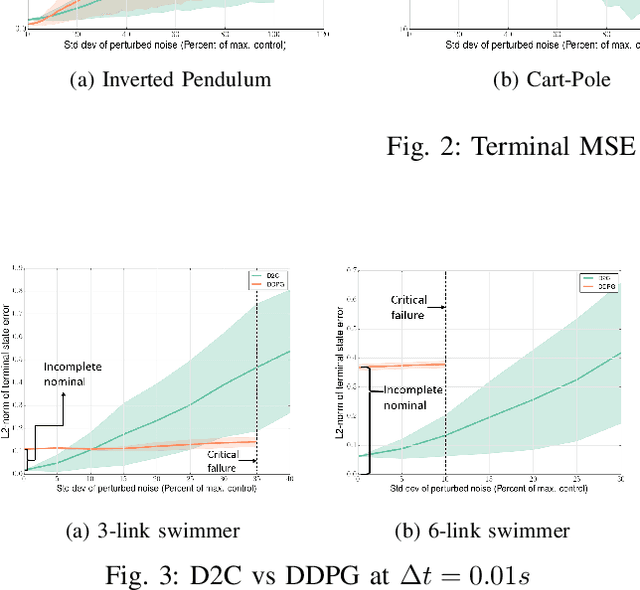
This paper addresses the problem of learning the optimal feedback policy for a nonlinear stochastic dynamical system with continuous state space, continuous action space and unknown dynamics. Feedback policies are complex objects that typically need a large dimensional parametrization, which makes Reinforcement Learning algorithms that search for an optimum in this large parameter space, sample inefficient and subject to high variance. We propose a "decoupling" principle that drastically reduces the feedback parameter space while still remaining near-optimal to the fourth-order in a small noise parameter. Based on this principle, we propose a decoupled data-based control (D2C) algorithm that addresses the stochastic control problem: first, an open-loop deterministic trajectory optimization problem is solved using a black-box simulation model of the dynamical system. Then, a linear closed-loop control is developed around this nominal trajectory using only a simulation model. Empirical evidence suggests significant reduction in training time, as well as the training variance, compared to other state of the art Reinforcement Learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge