Feedback Motion Planning Under Non-Gaussian Uncertainty and Non-Convex State Constraints
Paper and Code
Jan 12, 2016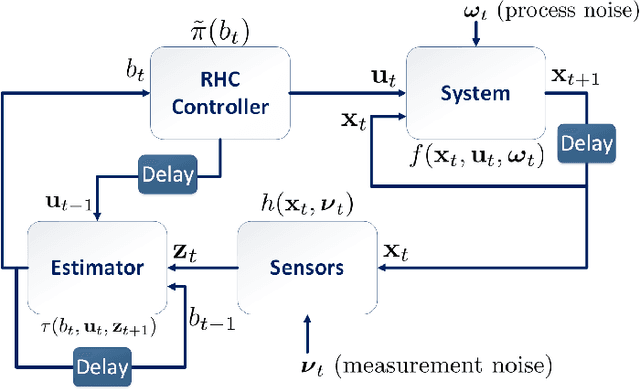
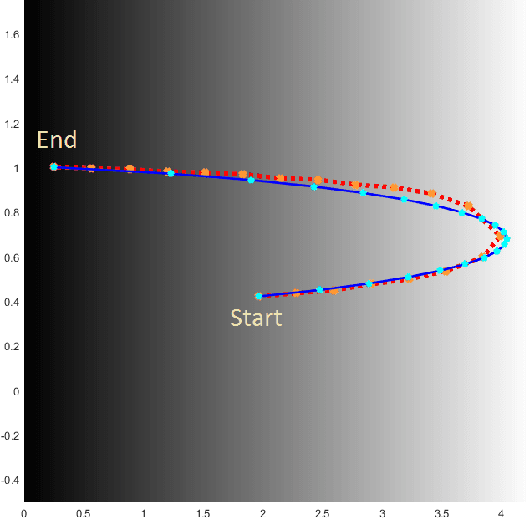


Planning under process and measurement uncertainties is a challenging problem. In its most general form it can be modeled as a Partially Observed Markov Decision Process (POMDP) problem. However POMDPs are generally difficult to solve when the underlying spaces are continuous, particularly when beliefs are non-Gaussian, and the difficulty is further exacerbated when there are also non-convex constraints on states. Existing algorithms to address such challenging POMDPs are expensive in terms of computation and memory. In this paper, we provide a feedback policy in non-Gaussian belief space via solving a convex program for common non-linear observation models. The solution involves a Receding Horizon Control strategy using particle filters for the non-Gaussian belief representation. We develop a way of capturing non-convex constraints in the state space and adapt the optimization to incorporate such constraints, as well. A key advantage of this method is that it does not introduce additional variables in the optimization problem and is therefore more scalable than existing constrained problems in belief space. We demonstrate the performance of the method on different scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge