Decentralized State Estimation via a Hybrid of Consensus and Covariance intersection

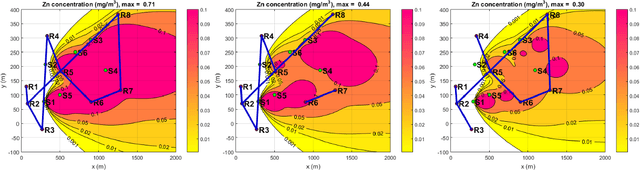
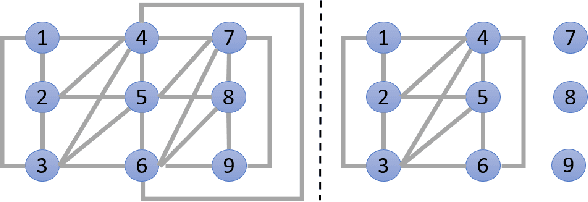
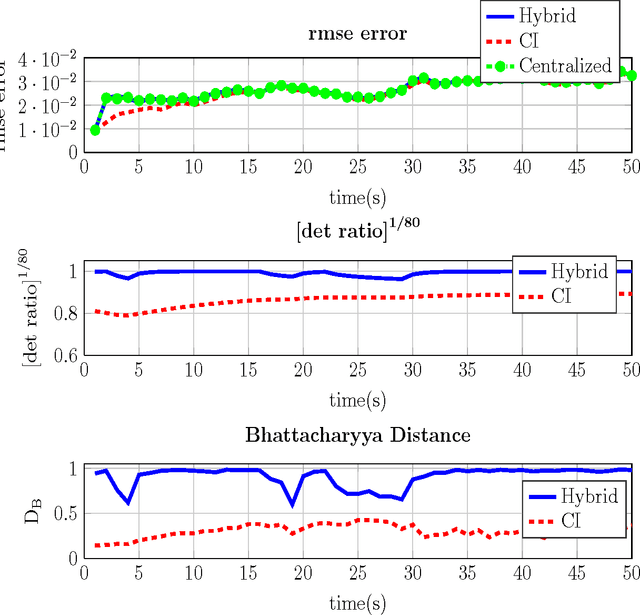
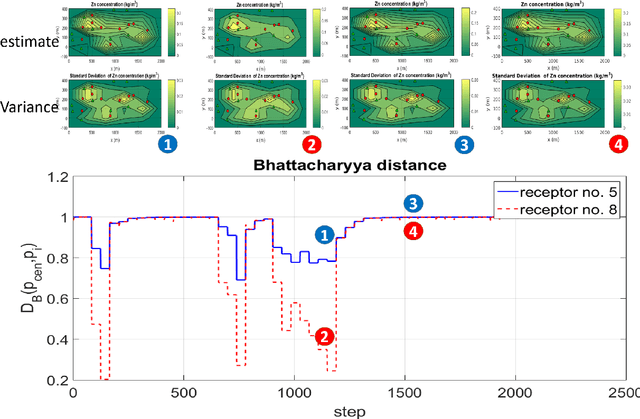
This paper presents a new recursive information consensus filter for decentralized dynamic-state estimation. No structure is assumed about the topology of the network and local estimators are assumed to have access only to local information. The network need not be connected at all times. Consensus over priors which might become correlated is performed through Covariance Intersection (CI) and consensus over new information is handled using weights based on a Metropolis Hastings Markov Chains. We establish bounds for estimation performance and show that our method produces unbiased conservative estimates that are better than CI. The performance of the proposed method is evaluated and compared with competing algorithms on an atmospheric dispersion problem.

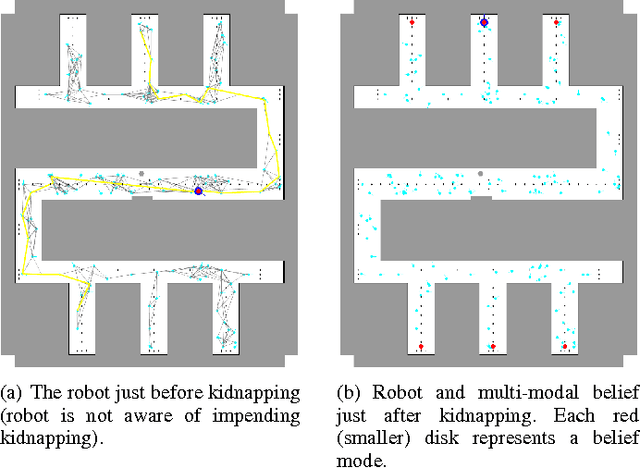
Motion Planning for Global Localization in Non-Gaussian Belief Spaces

This paper presents a method for motion planning under uncertainty to deal with situations where ambiguous data associations result in a multimodal hypothesis on the robot state. In the global localization problem, sometimes referred to as the "lost or kidnapped robot problem", given little to no a priori pose information, the localization algorithm should recover the correct pose of a mobile robot with respect to a global reference frame. We present a Receding Horizon approach, to plan actions that sequentially disambiguate a multimodal belief to achieve tight localization on the correct pose in finite time, i.e., converge to a unimodal belief. Experimental results are presented using a physical ground robot operating in an artificial maze-like environment. We demonstrate two runs wherein the robot is given no a priori information about its initial pose and the planner is tasked to localize the robot.

Feedback Motion Planning Under Non-Gaussian Uncertainty and Non-Convex State Constraints

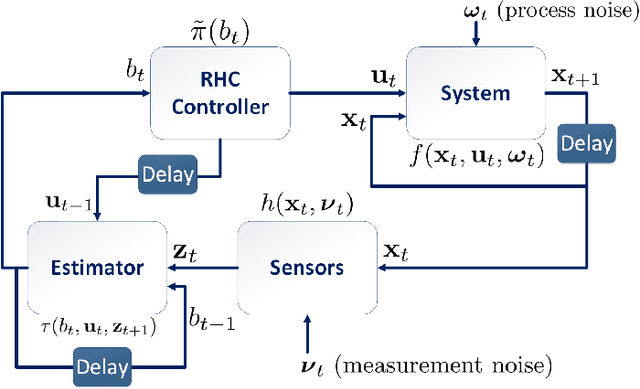
Planning under process and measurement uncertainties is a challenging problem. In its most general form it can be modeled as a Partially Observed Markov Decision Process (POMDP) problem. However POMDPs are generally difficult to solve when the underlying spaces are continuous, particularly when beliefs are non-Gaussian, and the difficulty is further exacerbated when there are also non-convex constraints on states. Existing algorithms to address such challenging POMDPs are expensive in terms of computation and memory. In this paper, we provide a feedback policy in non-Gaussian belief space via solving a convex program for common non-linear observation models. The solution involves a Receding Horizon Control strategy using particle filters for the non-Gaussian belief representation. We develop a way of capturing non-convex constraints in the state space and adapt the optimization to incorporate such constraints, as well. A key advantage of this method is that it does not introduce additional variables in the optimization problem and is therefore more scalable than existing constrained problems in belief space. We demonstrate the performance of the method on different scenarios.

Motion Planning in Non-Gaussian Belief Spaces : The Case of a Kidnapped Robot

Planning under uncertainty is a key requirement for physical systems due to the noisy nature of actuators and sensors. Using a belief space approach, planning solutions tend to generate actions that result in information seeking behavior which reduce state uncertainty. While recent work has dealt with planning for Gaussian beliefs, for many cases, a multi-modal belief is a more accurate representation of the underlying belief. This is particularly true in environments with information symmetry that cause uncertain data associations which naturally lead to a multi-modal hypothesis on the state. Thus, a planner cannot simply base actions on the most-likely state. We propose an algorithm that uses a Receding Horizon Planning approach to plan actions that sequentially disambiguate the multi-modal belief to a uni-modal Gaussian and achieve tight localization on the true state, called a Multi-Modal Motion Planner (M3P). By combining a Gaussian sampling-based belief space planner with M3P, and introducing a switching behavior in the planner and belief representation, we present a holistic end-to-end solution for the belief space planning problem. Simulation results for a 2D ground robot navigation problem are presented that demonstrate our method's performance.