Stochastic Feedback Control of Systems with Unknown Nonlinear Dynamics
Paper and Code
May 27, 2017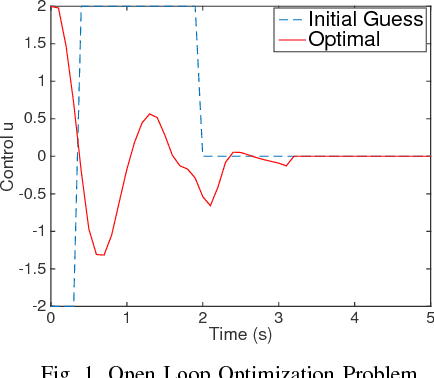


This paper studies the stochastic optimal control problem for systems with unknown dynamics. First, an open-loop deterministic trajectory optimization problem is solved without knowing the explicit form of the dynamical system. Next, a Linear Quadratic Gaussian (LQG) controller is designed for the nominal trajectory-dependent linearized system, such that under a small noise assumption, the actual states remain close to the optimal trajectory. The trajectory-dependent linearized system is identified using input-output experimental data consisting of the impulse responses of the nominal system. A computational example is given to illustrate the performance of the proposed approach.
* 7 pages, 7 figures, submitted to 56th IEEE Conference on Decision and
Control (CDC), 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge