Belief Space Planning Simplified: Trajectory-Optimized LQG (T-LQG) (Extended Report)
Paper and Code
Aug 11, 2016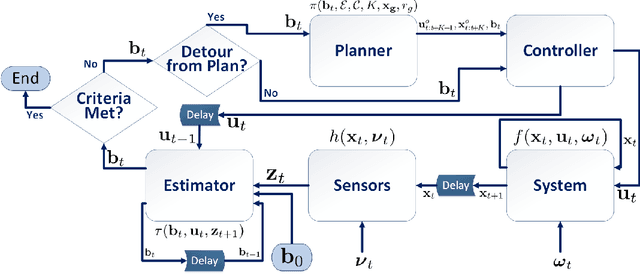
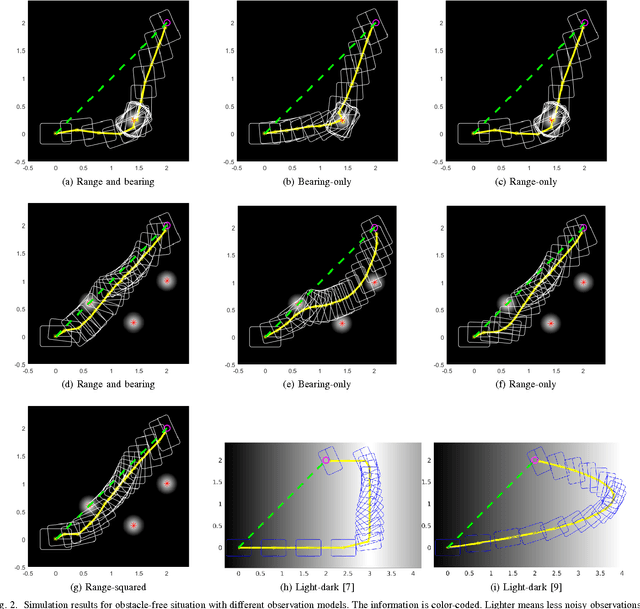
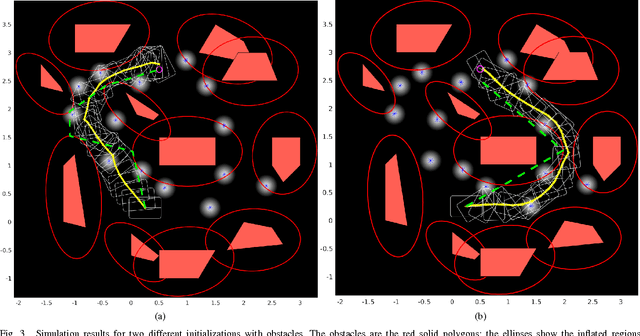
Planning under motion and observation uncertainties requires solution of a stochastic control problem in the space of feedback policies. In this paper, we reduce the general (n^2+n)-dimensional belief space planning problem to an (n)-dimensional problem by obtaining a Linear Quadratic Gaussian (LQG) design with the best nominal performance. Then, by taking the underlying trajectory of the LQG controller as the decision variable, we pose a coupled design of trajectory, estimator, and controller design through a Non-Linear Program (NLP) that can be solved by a general NLP solver. We prove that under a first-order approximation and a careful usage of the separation principle, our approximations are valid. We give an analysis on the existing major belief space planning methods and show that our algorithm has the lowest computational burden. Finally, we extend our solution to contain general state and control constraints. Our simulation results support our design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge