A Separation-Based Design to Data-Driven Control for Large-Scale Partially Observed Systems
Paper and Code
Jul 11, 2017
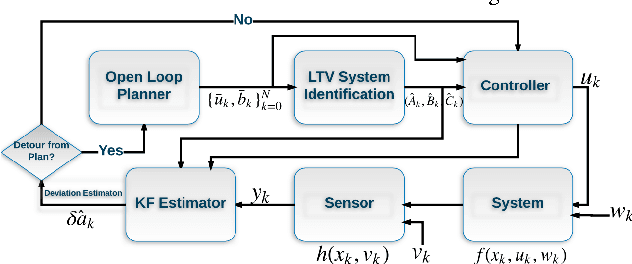

This paper studies the partially observed stochastic optimal control problem for systems with state dynamics governed by Partial Differential Equations (PDEs) that leads to an extremely large problem. First, an open-loop deterministic trajectory optimization problem is solved using a black box simulation model of the dynamical system. Next, a Linear Quadratic Gaussian (LQG) controller is designed for the nominal trajectory-dependent linearized system, which is identified using input-output experimental data consisting of the impulse responses of the optimized nominal system. A computational nonlinear heat example is used to illustrate the performance of the approach.
* 3 pages, 6 figures, In Robotics: Science and Systems (RSS) 2017
Workshop of "POMDPs in Robotics: State of The Art, Challenges, and
Opportunities"
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge