Near-Optimal Belief Space Planning via T-LQG
Paper and Code
Jul 10, 2017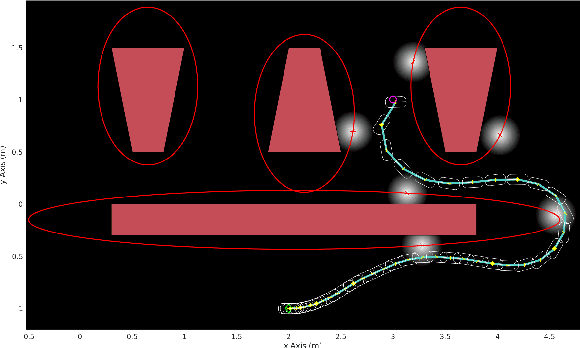
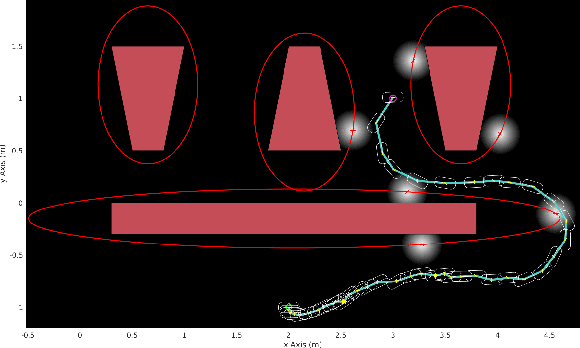
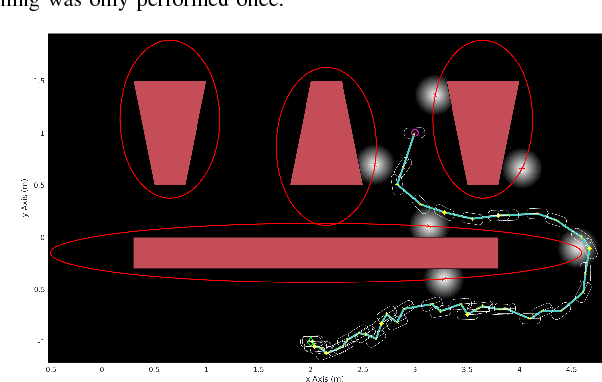
We consider the problem of planning under observation and motion uncertainty for nonlinear robotics systems. Determining the optimal solution to this problem, generally formulated as a Partially Observed Markov Decision Process (POMDP), is computationally intractable. We propose a Trajectory-optimized Linear Quadratic Gaussian (T-LQG) approach that leads to quantifiably near-optimal solutions for the POMDP problem. We provide a novel "separation principle" for the design of an optimal nominal open-loop trajectory followed by an optimal feedback control law, which provides a near-optimal feedback control policy for belief space planning problems involving a polynomial order of calculations of minimum order.
* 3 pages, 3 figures, In Robotics: Science and Systems (RSS) 2017
Workshop of "POMDPs in Robotics: State of The Art, Challenges, and
Opportunities"
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge