Solving a class of non-convex min-max games using adaptive momentum methods
Paper and Code
Apr 26, 2021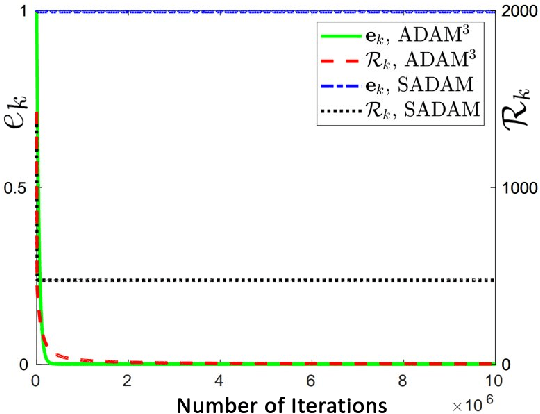
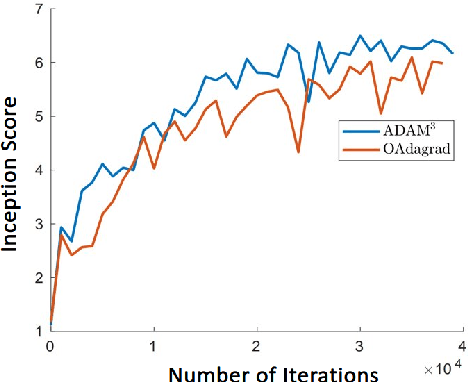

Adaptive momentum methods have recently attracted a lot of attention for training of deep neural networks. They use an exponential moving average of past gradients of the objective function to update both search directions and learning rates. However, these methods are not suited for solving min-max optimization problems that arise in training generative adversarial networks. In this paper, we propose an adaptive momentum min-max algorithm that generalizes adaptive momentum methods to the non-convex min-max regime. Further, we establish non-asymptotic rates of convergence for the proposed algorithm when used in a reasonably broad class of non-convex min-max optimization problems. Experimental results illustrate its superior performance vis-a-vis benchmark methods for solving such problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge