CombiGraph-Vis: A Curated Multimodal Olympiad Benchmark for Discrete Mathematical Reasoning

State-of-the-art (SOTA) LLMs have progressed from struggling on proof-based Olympiad problems to solving most of the IMO 2025 problems, with leading systems reportedly handling 5 of 6 problems. Given this progress, we assess how well these models can grade proofs: detecting errors, judging their severity, and assigning fair scores beyond binary correctness. We study proof-analysis capabilities using a corpus of 90 Gemini 2.5 Pro-generated solutions that we grade on a 1-4 scale with detailed error annotations, and on MathArena solution sets for IMO/USAMO 2025 scored on a 0-7 scale. Our analysis shows that models can reliably flag incorrect (including subtly incorrect) solutions but exhibit calibration gaps in how partial credit is assigned. To address this, we introduce agentic workflows that extract and analyze reference solutions and automatically derive problem-specific rubrics for a multi-step grading process. We instantiate and compare different design choices for the grading workflows, and evaluate their trade-offs. Across our annotated corpus and MathArena, our proposed workflows achieve higher agreement with human grades and more consistent handling of partial credit across metrics. We release all code, data, and prompts/logs to facilitate future research.

Brains vs. Bytes: Evaluating LLM Proficiency in Olympiad Mathematics

Recent advancements in large language models (LLMs) have shown impressive progress in mathematical reasoning tasks. However, current evaluation benchmarks predominantly focus on the accuracy of final answers, often overlooking the logical rigor crucial for mathematical problem-solving. The claim that state-of-the-art LLMs can solve Math Olympiad-level problems requires closer examination. To explore this, we conducted both qualitative and quantitative human evaluations of proofs generated by LLMs, and developed a schema for automatically assessing their reasoning capabilities. Our study reveals that current LLMs fall significantly short of solving challenging Olympiad-level problems and frequently fail to distinguish correct mathematical reasoning from clearly flawed solutions. We also found that occasional correct final answers provided by LLMs often result from pattern recognition or heuristic shortcuts rather than genuine mathematical reasoning. These findings underscore the substantial gap between LLM performance and human expertise in advanced mathematical reasoning and highlight the importance of developing benchmarks that prioritize the rigor and coherence of mathematical arguments rather than merely the correctness of final answers.

Regression with Large Language Models for Materials and Molecular Property Prediction

We demonstrate the ability of large language models (LLMs) to perform material and molecular property regression tasks, a significant deviation from the conventional LLM use case. We benchmark the Large Language Model Meta AI (LLaMA) 3 on several molecular properties in the QM9 dataset and 24 materials properties. Only composition-based input strings are used as the model input and we fine tune on only the generative loss. We broadly find that LLaMA 3, when fine-tuned using the SMILES representation of molecules, provides useful regression results which can rival standard materials property prediction models like random forest or fully connected neural networks on the QM9 dataset. Not surprisingly, LLaMA 3 errors are 5-10x higher than those of the state-of-the-art models that were trained using far more granular representation of molecules (e.g., atom types and their coordinates) for the same task. Interestingly, LLaMA 3 provides improved predictions compared to GPT-3.5 and GPT-4o. This work highlights the versatility of LLMs, suggesting that LLM-like generative models can potentially transcend their traditional applications to tackle complex physical phenomena, thus paving the way for future research and applications in chemistry, materials science and other scientific domains.

A Hybrid-Order Distributed SGD Method for Non-Convex Optimization to Balance Communication Overhead, Computational Complexity, and Convergence Rate

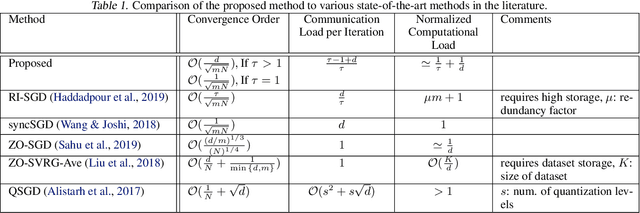
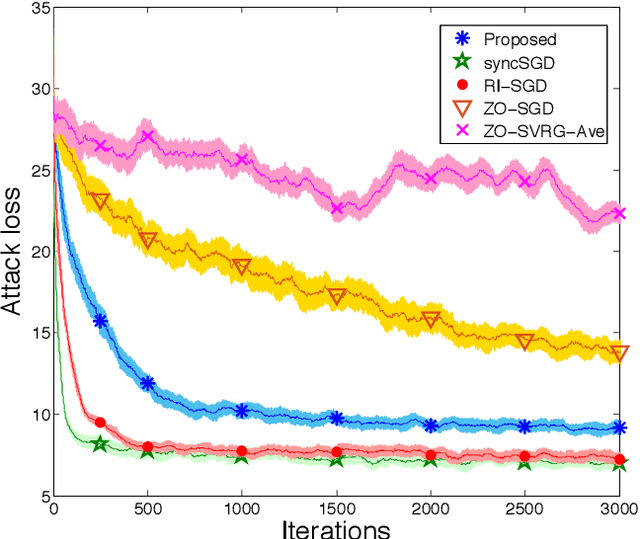
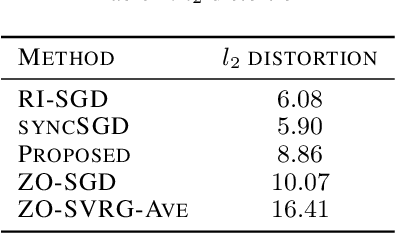
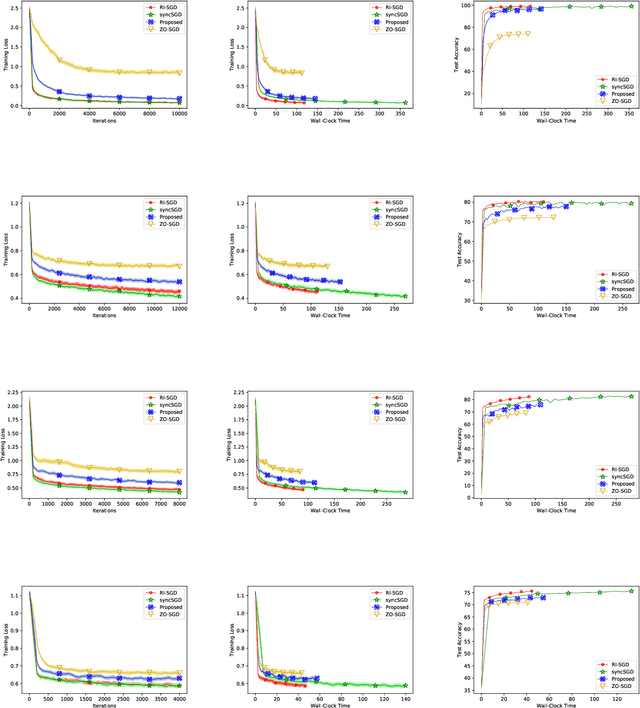
In this paper, we propose a method of distributed stochastic gradient descent (SGD), with low communication load and computational complexity, and still fast convergence. To reduce the communication load, at each iteration of the algorithm, the worker nodes calculate and communicate some scalers, that are the directional derivatives of the sample functions in some \emph{pre-shared directions}. However, to maintain accuracy, after every specific number of iterations, they communicate the vectors of stochastic gradients. To reduce the computational complexity in each iteration, the worker nodes approximate the directional derivatives with zeroth-order stochastic gradient estimation, by performing just two function evaluations rather than computing a first-order gradient vector. The proposed method highly improves the convergence rate of the zeroth-order methods, guaranteeing order-wise faster convergence. Moreover, compared to the famous communication-efficient methods of model averaging (that perform local model updates and periodic communication of the gradients to synchronize the local models), we prove that for the general class of non-convex stochastic problems and with reasonable choice of parameters, the proposed method guarantees the same orders of communication load and convergence rate, while having order-wise less computational complexity. Experimental results on various learning problems in neural networks applications demonstrate the effectiveness of the proposed approach compared to various state-of-the-art distributed SGD methods.

Towards Deployment of Robust AI Agents for Human-Machine Partnerships

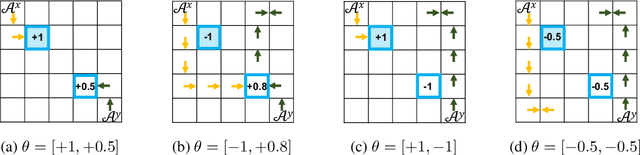
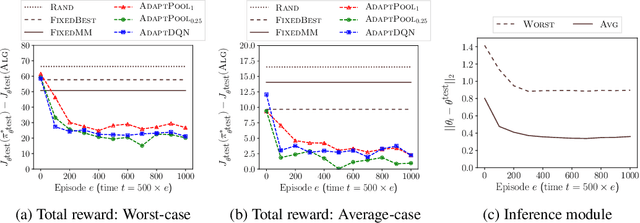
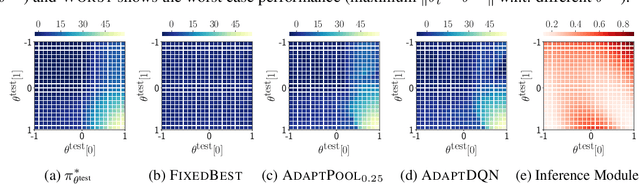
We study the problem of designing AI agents that can robustly cooperate with people in human-machine partnerships. Our work is inspired by real-life scenarios in which an AI agent, e.g., a virtual assistant, has to cooperate with new users after its deployment. We model this problem via a parametric MDP framework where the parameters correspond to a user's type and characterize her behavior. In the test phase, the AI agent has to interact with a user of unknown type. Our approach to designing a robust AI agent relies on observing the user's actions to make inferences about the user's type and adapting its policy to facilitate efficient cooperation. We show that without being adaptive, an AI agent can end up performing arbitrarily bad in the test phase. We develop two algorithms for computing policies that automatically adapt to the user in the test phase. We demonstrate the effectiveness of our approach in solving a two-agent collaborative task.