Extended Deep Submodular Functions

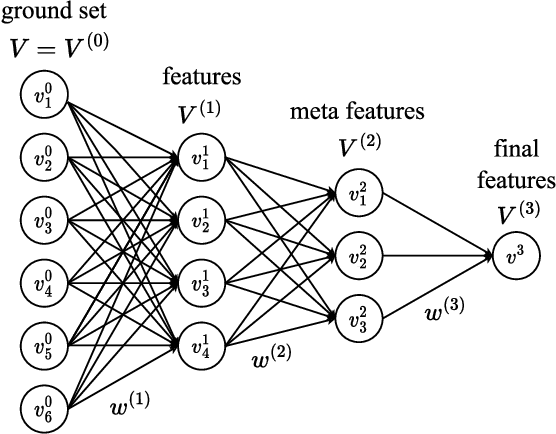
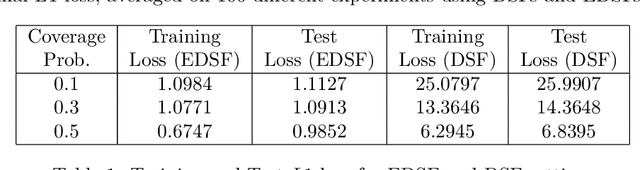
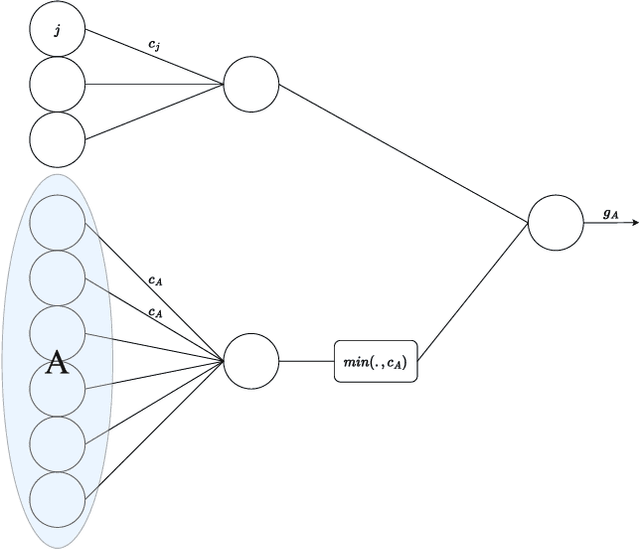
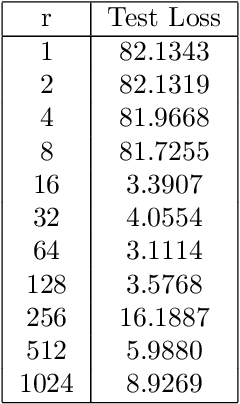
We introduce a novel category of set functions called Extended Deep Submodular functions (EDSFs), which are neural network-representable. EDSFs serve as an extension of Deep Submodular Functions (DSFs), inheriting crucial properties from DSFs while addressing innate limitations. It is known that DSFs can represent a limiting subset of submodular functions. In contrast, through an analysis of polymatroid properties, we establish that EDSFs possess the capability to represent all monotone submodular functions, a notable enhancement compared to DSFs. Furthermore, our findings demonstrate that EDSFs can represent any monotone set function, indicating the family of EDSFs is equivalent to the family of all monotone set functions. Additionally, we prove that EDSFs maintain the concavity inherent in DSFs when the components of the input vector are non-negative real numbers-an essential feature in certain combinatorial optimization problems. Through extensive experiments, we illustrate that EDSFs exhibit significantly lower empirical generalization error than DSFs in the learning of coverage functions. This suggests that EDSFs present a promising advancement in the representation and learning of set functions with improved generalization capabilities.

A Hybrid-Order Distributed SGD Method for Non-Convex Optimization to Balance Communication Overhead, Computational Complexity, and Convergence Rate

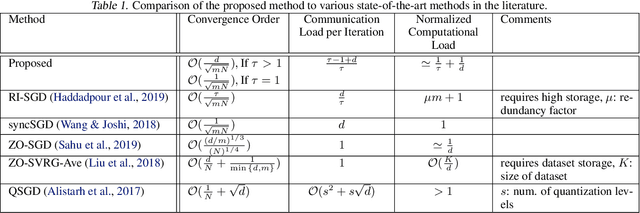
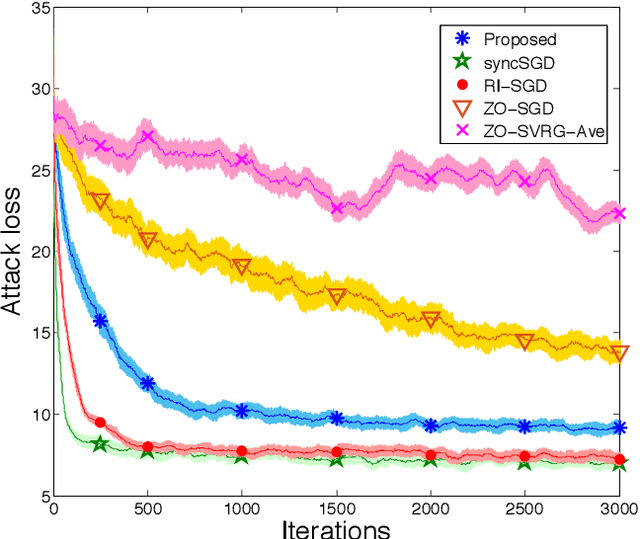
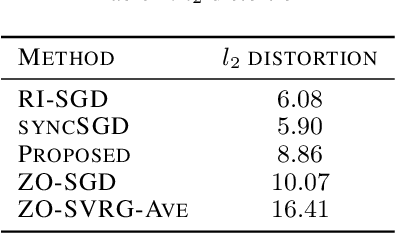
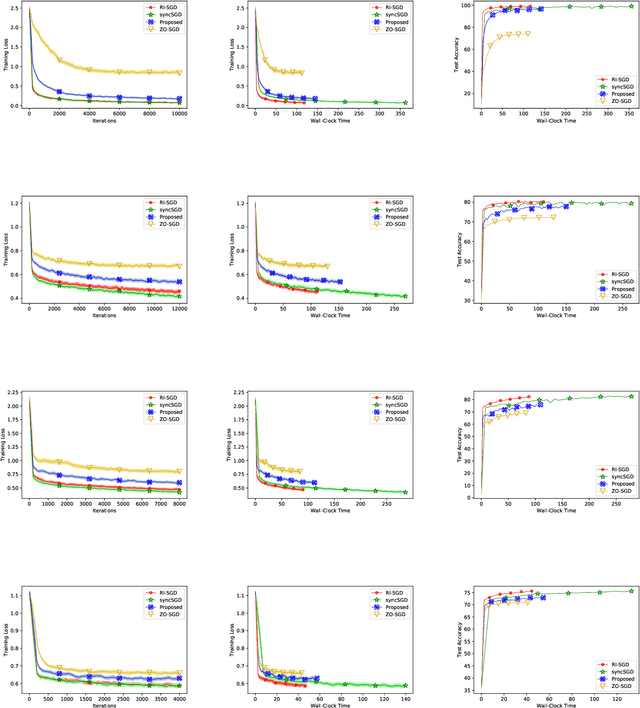
In this paper, we propose a method of distributed stochastic gradient descent (SGD), with low communication load and computational complexity, and still fast convergence. To reduce the communication load, at each iteration of the algorithm, the worker nodes calculate and communicate some scalers, that are the directional derivatives of the sample functions in some \emph{pre-shared directions}. However, to maintain accuracy, after every specific number of iterations, they communicate the vectors of stochastic gradients. To reduce the computational complexity in each iteration, the worker nodes approximate the directional derivatives with zeroth-order stochastic gradient estimation, by performing just two function evaluations rather than computing a first-order gradient vector. The proposed method highly improves the convergence rate of the zeroth-order methods, guaranteeing order-wise faster convergence. Moreover, compared to the famous communication-efficient methods of model averaging (that perform local model updates and periodic communication of the gradients to synchronize the local models), we prove that for the general class of non-convex stochastic problems and with reasonable choice of parameters, the proposed method guarantees the same orders of communication load and convergence rate, while having order-wise less computational complexity. Experimental results on various learning problems in neural networks applications demonstrate the effectiveness of the proposed approach compared to various state-of-the-art distributed SGD methods.