Theoretical Foundation of Flow-Based Time Series Generation: Provable Approximation, Generalization, and Efficiency

Recent studies suggest utilizing generative models instead of traditional auto-regressive algorithms for time series forecasting (TSF) tasks. These non-auto-regressive approaches involving different generative methods, including GAN, Diffusion, and Flow Matching for time series, have empirically demonstrated high-quality generation capability and accuracy. However, we still lack an appropriate understanding of how it processes approximation and generalization. This paper presents the first theoretical framework from the perspective of flow-based generative models to relieve the knowledge of limitations. In particular, we provide our insights with strict guarantees from three perspectives: $\textbf{Approximation}$, $\textbf{Generalization}$ and $\textbf{Efficiency}$. In detail, our analysis achieves the contributions as follows: $\bullet$ By assuming a general data model, the fitting of the flow-based generative models is confirmed to converge to arbitrary error under the universal approximation of Diffusion Transformer (DiT). $\bullet$ Introducing a polynomial-based regularization for flow matching, the generalization error thus be bounded since the generalization of polynomial approximation. $\bullet$ The sampling for generation is considered as an optimization process, we demonstrate its fast convergence with updating standard first-order gradient descent of some objective.

ParallelComp: Parallel Long-Context Compressor for Length Extrapolation

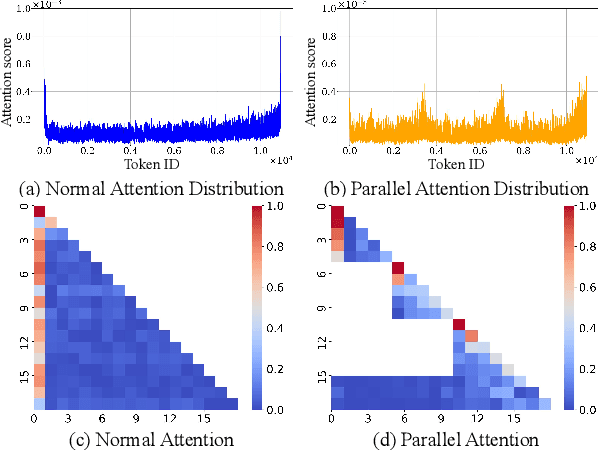
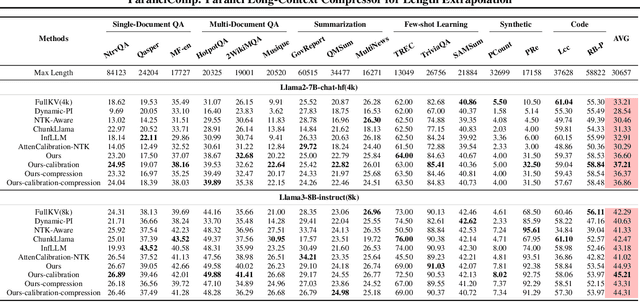
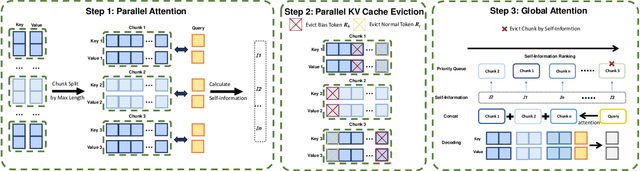
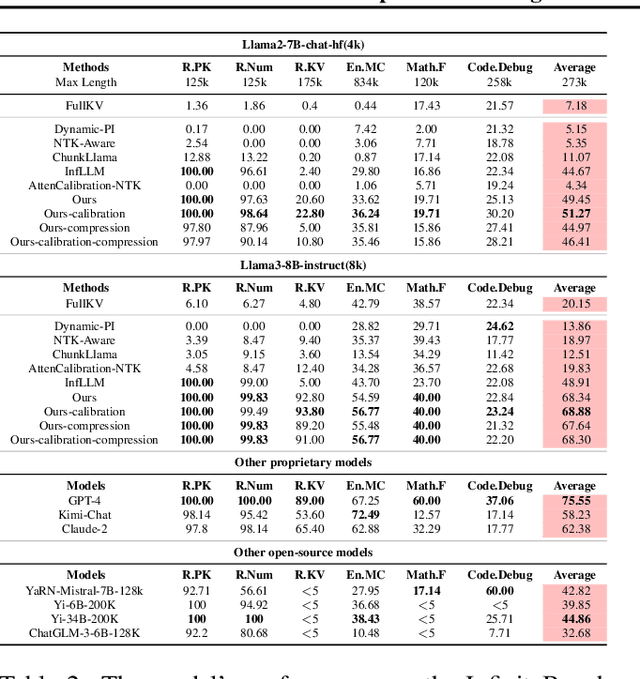
Efficiently handling long contexts is crucial for large language models (LLMs). While rotary position embeddings (RoPEs) enhance length generalization, effective length extrapolation remains challenging and often requires costly fine-tuning. In contrast, recent training-free approaches suffer from the attention sink phenomenon, leading to severe performance degradation. In this paper, we introduce ParallelComp, a novel training-free method for long-context extrapolation that extends LLMs' context length from 4K to 128K while maintaining high throughput and preserving perplexity, and integrates seamlessly with Flash Attention. Our analysis offers new insights into attention biases in parallel attention mechanisms and provides practical solutions to tackle these challenges. To mitigate the attention sink issue, we propose an attention calibration strategy that reduces biases, ensuring more stable long-range attention. Additionally, we introduce a chunk eviction strategy to efficiently manage ultra-long contexts on a single A100 80GB GPU. To further enhance efficiency, we propose a parallel KV cache eviction technique, which improves chunk throughput by 1.76x, thereby achieving a 23.50x acceleration in the prefilling stage with negligible performance loss due to attention calibration. Furthermore, ParallelComp achieves 91.17% of GPT-4's performance on long-context tasks using an 8B model trained on 8K-length context, outperforming powerful closed-source models such as Claude-2 and Kimi-Chat.

Curse of Attention: A Kernel-Based Perspective for Why Transformers Fail to Generalize on Time Series Forecasting and Beyond

The application of transformer-based models on time series forecasting (TSF) tasks has long been popular to study. However, many of these works fail to beat the simple linear residual model, and the theoretical understanding of this issue is still limited. In this work, we propose the first theoretical explanation of the inefficiency of transformers on TSF tasks. We attribute the mechanism behind it to {\bf Asymmetric Learning} in training attention networks. When the sign of the previous step is inconsistent with the sign of the current step in the next-step-prediction time series, attention fails to learn the residual features. This makes it difficult to generalize on out-of-distribution (OOD) data, especially on the sign-inconsistent next-step-prediction data, with the same representation pattern, whereas a linear residual network could easily accomplish it. We hope our theoretical insights provide important necessary conditions for designing the expressive and efficient transformer-based architecture for practitioners.

Unlocking the Theory Behind Scaling 1-Bit Neural Networks

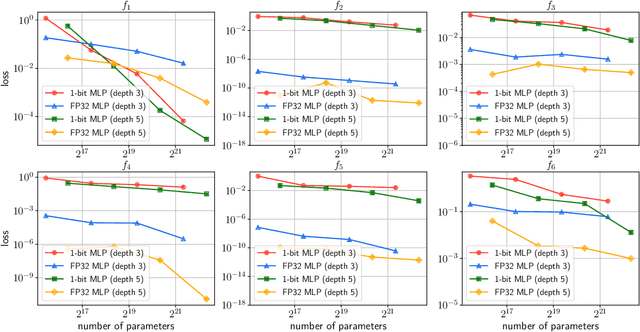
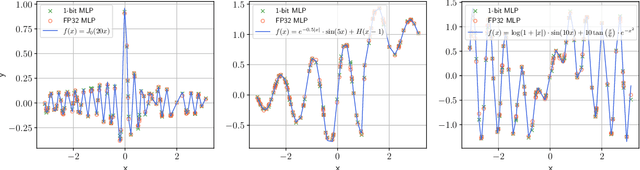
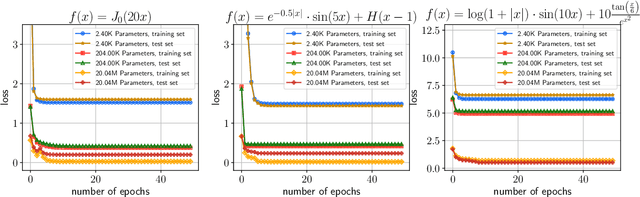
Recently, 1-bit Large Language Models (LLMs) have emerged, showcasing an impressive combination of efficiency and performance that rivals traditional LLMs. Research by Wang et al. (2023); Ma et al. (2024) indicates that the performance of these 1-bit LLMs progressively improves as the number of parameters increases, hinting at the potential existence of a Scaling Law for 1-bit Neural Networks. In this paper, we present the first theoretical result that rigorously establishes this scaling law for 1-bit models. We prove that, despite the constraint of weights restricted to $\{-1, +1\}$, the dynamics of model training inevitably align with kernel behavior as the network width grows. This theoretical breakthrough guarantees convergence of the 1-bit model to an arbitrarily small loss as width increases. Furthermore, we introduce the concept of the generalization difference, defined as the gap between the outputs of 1-bit networks and their full-precision counterparts, and demonstrate that this difference maintains a negligible level as network width scales. Building on the work of Kaplan et al. (2020), we conclude by examining how the training loss scales as a power-law function of the model size, dataset size, and computational resources utilized for training. Our findings underscore the promising potential of scaling 1-bit neural networks, suggesting that int1 could become the standard in future neural network precision.

Toward Infinite-Long Prefix in Transformer

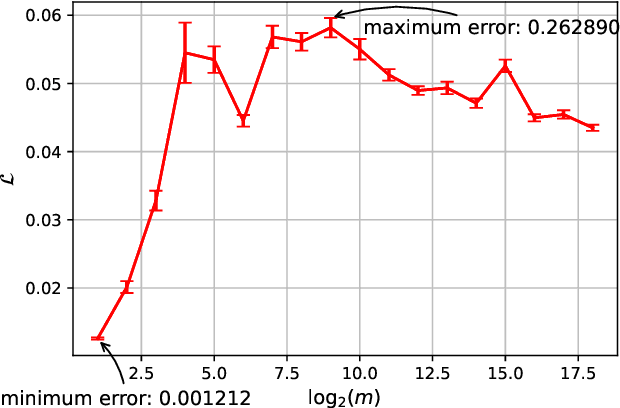
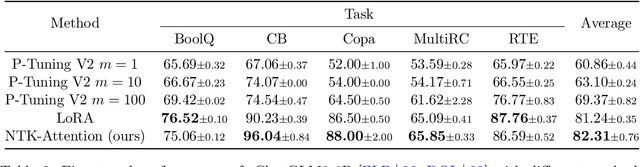
Prompting and contextual-based fine-tuning methods, which we call Prefix Learning, have been proposed to enhance the performance of language models on various downstream tasks that can match full parameter fine-tuning. There remains a limited theoretical understanding of how these methods work. In this paper, we aim to relieve this limitation by studying the learning ability of Prefix Learning from the perspective of prefix length. In particular, we approximate the infinite-long Prefix Learning optimization process by the Neural Tangent Kernel (NTK) technique. We formulate and solve it as a learning problem of the infinite-long prefix in a one-layer attention network. Our results confirm the over-parameterization property and arbitrary small loss convergence guarantee of the infinite-long Prefix Learning in attention. To the implementation end, we propose our NTK-Attention method, which is "equivalent" to attention computation with arbitrary prefix length efficiently. Its time complexity mainly depends on the sub-quadratic of input length (without prefix), and our method only requires $d^2 + d$ extra parameters for representation, where $d$ is the feature dimension. In addition, we conducted experiments that compare our NTK-Attention with full parameters fine-tuning, LoRA, and P-Tuning V2 methods across vision or natural language datasets. The results indicate our approach may be a promising parameter-efficient-fine-tuning method since it has demonstrated superior performance in numerous scenarios. Our code can be found at \url{https://github.com/ChristianYang37/chiwun/tree/main/src/NTK-Attention}.

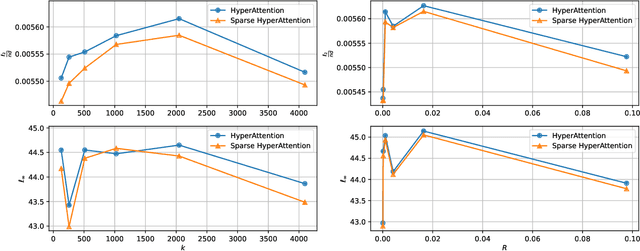
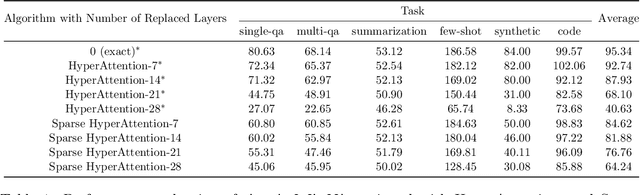
Attention is Naturally Sparse with Gaussian Distributed Input

The computational intensity of Large Language Models (LLMs) is a critical bottleneck, primarily due to the $O(n^2)$ complexity of the attention mechanism in transformer architectures. Addressing this, sparse attention emerges as a key innovation, aiming to reduce computational load while maintaining model performance. This study presents a rigorous theoretical analysis of the sparsity in attention scores within LLMs, particularly under the framework of Gaussian inputs. By establishing a set of foundational assumptions and employing a methodical theoretical approach, we unravel the intrinsic characteristics of attention score sparsity and its implications on computational efficiency. Our main contribution lies in providing a detailed theoretical examination of how sparsity manifests in attention mechanisms, offering insights into the potential trade-offs between computational savings and model effectiveness. This work not only advances our understanding of sparse attention but also provides a scaffold for future research in optimizing the computational frameworks of LLMs, paving the way for more scalable and efficient AI systems.

Enhancing Stochastic Gradient Descent: A Unified Framework and Novel Acceleration Methods for Faster Convergence

Based on SGD, previous works have proposed many algorithms that have improved convergence speed and generalization in stochastic optimization, such as SGDm, AdaGrad, Adam, etc. However, their convergence analysis under non-convex conditions is challenging. In this work, we propose a unified framework to address this issue. For any first-order methods, we interpret the updated direction $g_t$ as the sum of the stochastic subgradient $\nabla f_t(x_t)$ and an additional acceleration term $\frac{2|\langle v_t, \nabla f_t(x_t) \rangle|}{\|v_t\|_2^2} v_t$, thus we can discuss the convergence by analyzing $\langle v_t, \nabla f_t(x_t) \rangle$. Through our framework, we have discovered two plug-and-play acceleration methods: \textbf{Reject Accelerating} and \textbf{Random Vector Accelerating}, we theoretically demonstrate that these two methods can directly lead to an improvement in convergence rate.

One Pass Streaming Algorithm for Super Long Token Attention Approximation in Sublinear Space

Deploying Large Language Models (LLMs) in streaming applications that involve long contexts, particularly for extended dialogues and text analysis, is of paramount importance but presents two significant challenges. Firstly, the memory consumption is substantial during the decoding phase due to the caching of Key and Value states (KV) of previous tokens. Secondly, attention computation is time-consuming with a time complexity of $O(n^2)$ for the generation of each token. In recent OpenAI DevDay (Nov 6, 2023), OpenAI released a new model that is able to support a 128K-long document, in our paper, we focus on the memory-efficient issue when context length $n$ is much greater than 128K ($n \gg 2^d$). Considering a single-layer self-attention with Query, Key, and Value matrices $Q, K, V \in \mathbb{R}^{n \times d}$, the polynomial method approximates the attention output $T \in \mathbb{R}^{n \times d}$. It accomplishes this by constructing $U_1, U_2 \in \mathbb{R}^{n \times t}$ to expedite attention ${\sf Attn}(Q, K, V)$ computation within $n^{1+o(1)}$ time executions. Despite this, storing the Key and Value matrices $K, V \in \mathbb{R}^{n \times d}$ still necessitates $O( n d)$ space, leading to significant memory usage. In response to these challenges, we introduce a new algorithm that only reads one pass of the data in streaming fashion. This method employs sublinear space $o(n)$ to store three sketch matrices, alleviating the need for exact $K, V$ storage. Notably, our algorithm exhibits exceptional memory-efficient performance with super-long tokens. As the token length $n$ increases, our error guarantee diminishes while the memory usage remains nearly constant. This unique attribute underscores the potential of our technique in efficiently handling LLMs in streaming applications.

A Theoretical Insight into Attack and Defense of Gradient Leakage in Transformer

The Deep Leakage from Gradient (DLG) attack has emerged as a prevalent and highly effective method for extracting sensitive training data by inspecting exchanged gradients. This approach poses a substantial threat to the privacy of individuals and organizations alike. This research presents a comprehensive analysis of the gradient leakage method when applied specifically to transformer-based models. Through meticulous examination, we showcase the capability to accurately recover data solely from gradients and rigorously investigate the conditions under which gradient attacks can be executed, providing compelling evidence. Furthermore, we reevaluate the approach of introducing additional noise on gradients as a protective measure against gradient attacks. To address this, we outline a theoretical proof that analyzes the associated privacy costs within the framework of differential privacy. Additionally, we affirm the convergence of the Stochastic Gradient Descent (SGD) algorithm under perturbed gradients. The primary objective of this study is to augment the understanding of gradient leakage attack and defense strategies while actively contributing to the development of privacy-preserving techniques specifically tailored for transformer-based models. By shedding light on the vulnerabilities and countermeasures associated with gradient leakage, this research aims to foster advancements in safeguarding sensitive data and upholding privacy in the context of transformer-based models.

Unmasking Transformers: A Theoretical Approach to Data Recovery via Attention Weights

In the realm of deep learning, transformers have emerged as a dominant architecture, particularly in natural language processing tasks. However, with their widespread adoption, concerns regarding the security and privacy of the data processed by these models have arisen. In this paper, we address a pivotal question: Can the data fed into transformers be recovered using their attention weights and outputs? We introduce a theoretical framework to tackle this problem. Specifically, we present an algorithm that aims to recover the input data $X \in \mathbb{R}^{d \times n}$ from given attention weights $W = QK^\top \in \mathbb{R}^{d \times d}$ and output $B \in \mathbb{R}^{n \times n}$ by minimizing the loss function $L(X)$. This loss function captures the discrepancy between the expected output and the actual output of the transformer. Our findings have significant implications for the Localized Layer-wise Mechanism (LLM), suggesting potential vulnerabilities in the model's design from a security and privacy perspective. This work underscores the importance of understanding and safeguarding the internal workings of transformers to ensure the confidentiality of processed data.