Unmasking Transformers: A Theoretical Approach to Data Recovery via Attention Weights
Paper and Code
Oct 19, 2023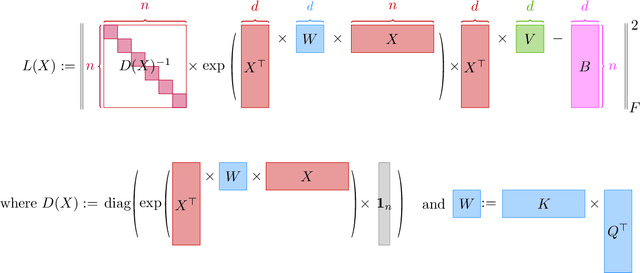

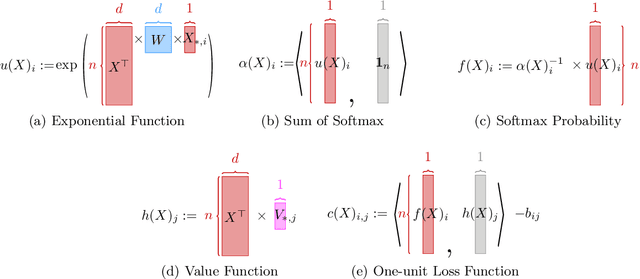

In the realm of deep learning, transformers have emerged as a dominant architecture, particularly in natural language processing tasks. However, with their widespread adoption, concerns regarding the security and privacy of the data processed by these models have arisen. In this paper, we address a pivotal question: Can the data fed into transformers be recovered using their attention weights and outputs? We introduce a theoretical framework to tackle this problem. Specifically, we present an algorithm that aims to recover the input data $X \in \mathbb{R}^{d \times n}$ from given attention weights $W = QK^\top \in \mathbb{R}^{d \times d}$ and output $B \in \mathbb{R}^{n \times n}$ by minimizing the loss function $L(X)$. This loss function captures the discrepancy between the expected output and the actual output of the transformer. Our findings have significant implications for the Localized Layer-wise Mechanism (LLM), suggesting potential vulnerabilities in the model's design from a security and privacy perspective. This work underscores the importance of understanding and safeguarding the internal workings of transformers to ensure the confidentiality of processed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge